Иногда у истоков нетривиальных открытий лежит игра, забава. Может ли бесконечная геометрическая фигура, созданная дизайнером, иметь практическую пользу для математики и техники? И при чём тут создатель кубика Рубика?
Перебирая комбинации равнобедренных и равносторонних треугольников, чередующихся в определённой последовательности, венгерский студент Даниэль Эрдели (в наши дни — известный дизайнер) в 70-х годах прошлого века создал удивительные спиральные орнаменты и пространственные формы. За много лет творческих поисков он разработал, руководствуясь принципом фрактального самоподобия, целый ряд таких объектов, названных спидронами (слово spidron отсылает к английским словам spider, «паук», и spiral, «спираль»).
Иногда у истоков нетривиальных открытий лежит игра, забава. Может ли бесконечная геометрическая фигура, созданная дизайнером, иметь практическую пользу для математики и техники? И при чём тут создатель кубика Рубика? »Нетрудно увидеть сходство спидронов с паутиной в тех случаях, когда многоугольник выступает внешним контуром спидронов. Фрактальное самоподобие проявляется в том, что фигура состоит из элементов, отдельные части кото- рой повторяют форму и свойства всей фигуры в целом, наделяя их свойством математической бесконечности.
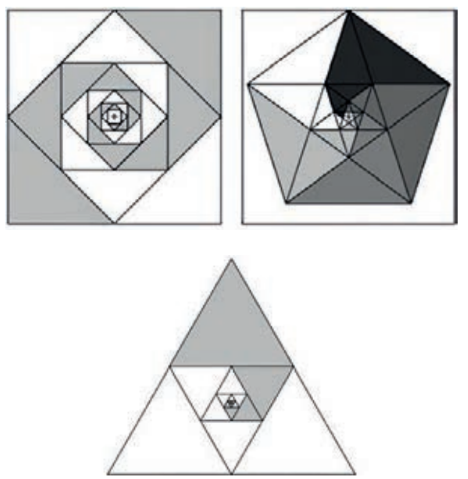
Тема перекликается с фрактальной геометрией, открытой Бенуа Мандельбортом в 1970-х: она описывает упорядоченный хаос природы и демонстрирует принцип бесконечного вложения самоподобных структур друг в друга на основе простых математических соотношений.
Треугольная салфетка Серпинского. Её построение начинается с равностороннего треугольника. Из него вырезается перевёрнутый центральный равносторонний треугольник со стороной, равной половине длины стороны исходного треугольника. Остаются три равносторонних треугольника со сторонами, вдвое меньше стороны исходного треугольника.
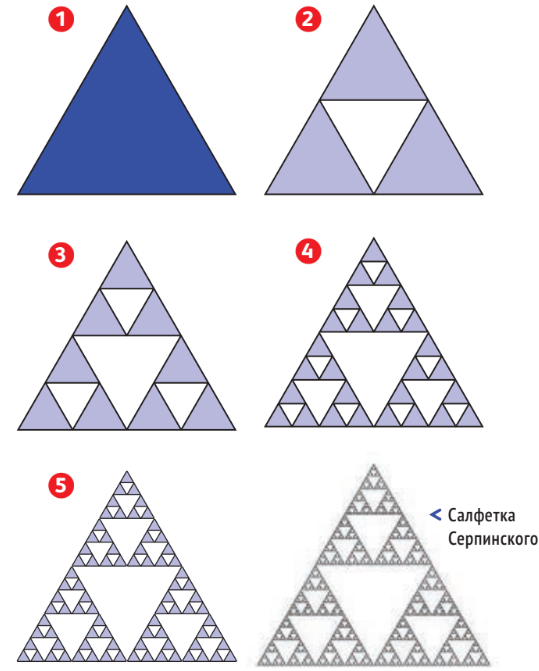
К ним также применяется операция удаления центрального треугольника, образуется девять треугольников, из которых, в свою очередь, тоже вырезается треугольник, и так до бесконечности.
Свойства спидронов
- Теоретически они не имеют завершения, но по факту их предметное воспроизведение ограничено незначительным пространством, которое нельзя будет использовать для их детализации.
- Площадь любого равностороннего треугольника в любом «плече» равна сумме площадей всех последующих меньших треугольников. Другими словами, в равносторонний треугольник можно вписать все остальные, которые строились после него.
- Если вырезать плоские спидроны из листового материала, например, из бумаги, и согнуть их по линиям узора, то они они превратятся в складчатую конструкцию, которая напоминает меха аккордеона.
- Различные варианты таким образом преобразованных плоских спидронов позволяют добиться создания самых разных рельефных поверхностей.
Щупальца или хвост?
При этом надо сказать, что первый спидрон Даниэль придумал ещё за несколько лет до того, на занятиях у преподавателя Иштвана Варга-Хайду в Профессиональном училище поли- графической промышленности. Ассоциативно первый спидрон похож на комбинацию из двух хвостов морского конька или щупалец осьминога.
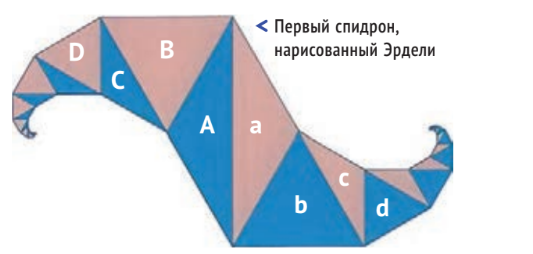
Спидрон. Заглавные буквы показывают четыре треугольника в одном «рукаве» спидрона. Строчные буквы показывают четыре начальных треугольника в другом «рукаве». Каждый рукав состоит из чередующихся равнобедренных (А, а, С, с) и равносторонних (В, b, D, d) треугольников.
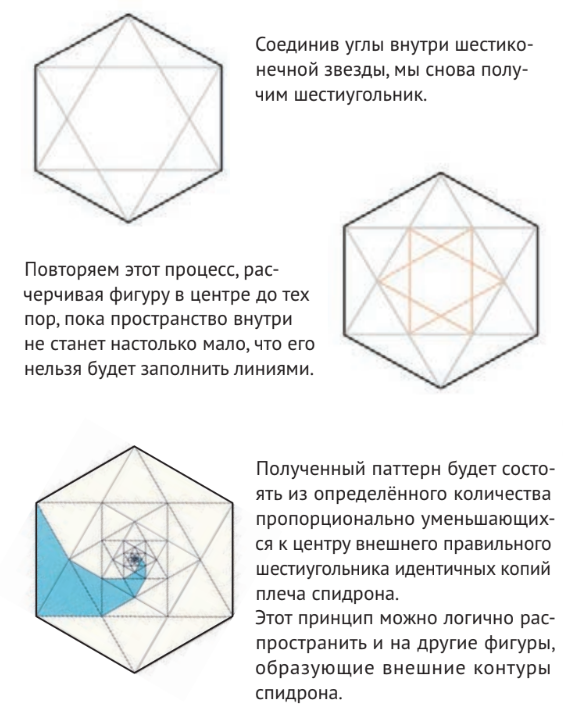
Каждый из двух рукавов показанного спидрона можно получить самостоятельно. Вначале надо начертить правильный шестиугольник, а далее соединить отрезками его углы таким образом, чтобы возникла шестиконечная звезда.
Спидроны интересны и искусству, и математике. Крейг С. Каплан — профессор Школы компьютерных наук Университета Ватерлоо из Канады — использует алгоритмы для создания необычных узоров. Здесь совсем не лишними будут знания компьютерной графики, геометрии, теории графов, теории симметрии, а также психологии зрительного восприятия. Его вписанные в окружность орнаменты из убывающих от центра к краю спидронов дают вам ощущение объёма и бесконечности.
Орнаменты
Интересно рассмотреть спидроны с точки зрения замощения плоскости. Речь в данном случае идёт о мозаичном покрытии поверхности без наслоений, или о паркетном замощении. Существует большое разнообразие таких форм.

Самые простые варианты паркетного замощения достигаются с использованием трёх правильных многоугольников — треугольника, квадрата и шестиугольника. Паркеты, состав- ленные из одинаковых правильных многоугольников, называют правильными паркетами. Покрытие с использованием спидронов представляет собой неклассический вариант замощения, «фрактальный». Способы замощения, в основе которых выступают спидроны, визуально созвучны мозаичным композициям нидерландского художника-графика Маурица Эшера.
От игрушки до солнечных панелей
Интересные сами по себе с абстрактно-научной и эстетической точек зрения, спидроны могут найти прикладное применение в качестве складных солнечных панелей или амортизаторов. А блоки в виде многогранников с рельефными спидронами на гранях могут представлять собой оригинальную деталь в составе детского строительного набора.
В научной литературе описаны также конструкции радиоантенн с использованием спидронов. Спидроны — пример того, как математический объект в руках дизайнера получил изящное воплощение. В этом факте нет противоречия! Умение в абстрактном распознать красивое и занимательное служит источником удивительных открытий.
Следующий этап развития спидронов — их трансформация в складчатые конструкции или рельефы. Для этого линии спирального узора превратили в рёбра, придав конструкции выпуклую форму. Так возникли рельефные поверхности, которые, в свою очередь, породили спидроны-многогранники.






