В повседневной жизни для обозначения чисел мы используем десятич- ную систему счисления. Она называется так потому, что в ней числа записываются с помощью десяти цифр от 0 до 9. Но существуют и другие способы записи. Один из них — двоичная система счисления.
НОЛЬ, ОДИН, ОДИН НОЛЬ
В двоичной системе используются всего две цифры — 0 и 1. Однако и ими можно записать сколь угодно большие числа. Записать числа 0 и 1 просто: есть соответствующие цифры. С числом 2 и всеми остальными уже сложнее. Как будет выглядеть 2 в двоичной системе? Вспомним, что когда мы последовательно увеличиваем число на 1 (получаем ряд 0, 1, 2, 3…), доходим до 9 (используем все цифры) и хотим получить число, на 1 большее, то мы записываем минимально возможную цифру 0 и слева от неё — единицу (10).
Аналогично следует поступить и при записи числа 2 в двоичной системе счисления — 10, только в данном случае о записанном числе нельзя сказать «десять» — это слово применимо только к десятичной системе. Нужно говорить «один ноль». Получить двоичное число, со- ответствующее десятичному числу 3 (на 1 большее, чем двоичное число 10), можем, заменив последний 0 на 1 — получим 11.

Говорить «одиннадцать» также неправильно, правильно: «один, один». Как быть со следующим десятичным числом — 4? Здесь тоже вспомним, что в десятичной системе после числа 99 (в двух разрядах записана максимально возможная цифра) идёт 100. Аналогично и в двоичной системе следующее за 11 число — 100 («один, ноль, ноль» — не «сто»!).
КАК ПОЛУЧИТЬ БОЛЬШОЕ ДВОИЧНОЕ ЧИСЛО?
А если нужно записать в двоичной системе число 47, 218 или ещё большее? Тут выписывание последовательных чисел не подойдёт. Существу- ют специальные методы перевода десятичных чисел в двоичные. Покажем один из них на при- мере числа 37. Разделим его нацело на 2. Затем разделим на 2 полученное частное (18), затем новое частное и т. д. до тех пор, пока частное не станет равно 1. При делении будем выписывать так же получающиеся остатки:
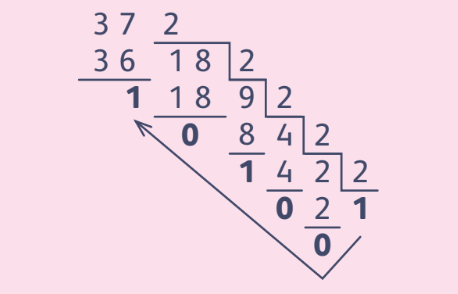
Результат получается выписыванием послед- него частного (1) и всех остатков в обратном порядке, то есть это 1001012 (цифры результата выделены полужирным начертанием). Нижний индекс 2 говорит о том, что число записано в двоичной системе счисления.
А НАОБОРОТ?
А как из двоичного числа получить соответствующее ему десятичное? Для ответа вспомним, как представить число в десятичной системе счисления. Например, число 2073 можно разложить так: 2073 = 2 × 1000 + 0 × 100 + 7 × 10 + 3 × 1 = = 2 × 103 + 1 × 102 + 7 × 101 + 3 × 100
То есть число 2073 состоит из 2 тысяч, 0 сотен, 7 десятков и 3 единиц. Значения 1 (100), 10 (101), 100 (102) и т. д. называют весом, или весомостью, того или иного разряда числа. Видно, что весомость разряда равна 10n, где n — номер разряда при условии, что последние нумеруются справа налево, начиная с нуля. В двоичной системе можно поступить так же. Пусть двоичное число равно 1101012. Чтобы получить его десятичный эквивалент:
●1 пронумеруем разряды заданного числа справа налево, начиная с нуля:

Если числа 1, 2, 4, … назвать «весомостью разрядов двоичных чисел», то, как и для десятичной системы, можем пред- ставить заданное число следующим образом: 1 × 32 + 1 × 16 + 0 × 8 × 1 × 4 + 0 × 2 + 1 × 1 = = 32 + 16 + 4 + 1 = 53 Полученная сумма и будет равна десятичному числу, со- ответствующему заданному двоичному. Итак, 1101012 = 5310. Можно так сформулировать правило перевода чисел из двоичной системы счисления в десятичную — необходимо сложить весомости тех двоичных разрядов, в которых записана цифра 1. При этом весомости разрядов (1, 2, 4, …) равны 10n, где n — номер разряда при нумерации разрядов справа налево, начиная с нуля.
Операция над числами
Арифметические операции над двоичными числами выполнять очень просто. Вот таблица сложения: 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 и 1 переносится в соседний старший разряд.
Пример:

Ещё проще в двоичной системе таблица умножения — она состоит всего из одной строки: 1 × 1 = 1 (Помните свои «проблемы» при заучивании таблицы умножения в десятичной системе?) При умножении многозначных двоичных чисел можно просто выписывать множимое в случае умножения на 1 и пропускать нули в множителе:

ПРИ ЧЁМ ТУТ КОМПЬЮТЕР?
Простота двоичной системы привела учёных и инженеров к мысли о том, что именно она должна быть использована в компьютерах. Ведь в них, как в технических устройствах, элементы могут находиться в двух состояниях (включено — выключено, ток идёт или не идёт, лампочка горит или не горит, напряжение высокое или низкое и т. п.). Одному из этих состояний можно условно сопоставить 1, другому — 0, то есть использовать цифры двоичной системы, и тогда информация будет фиксироваться, храниться, передаваться и обрабатываться в двоичном виде (хотя, конечно, сами цифры 0 и 1 в компьютерах нигде не записаны). Первую механическую вычислительную машину, использующую двоичную систему счисления, изготовил в конце 1930-х годов немец- кий инженер Конрад Цузце, а первый электронный компьютер такого типа — ЭНИАК — был разработан в 1945 году. Интересно, что впервые на возможность применения в вычислительных машинах двоичной системы счисления указал ещё в 1882 (!) году французский математик дуард Люка в книге «Занимательная математика». Он писал: «…эта система лучше всякой другой годилась бы для устройства арифметической машины…»
ПОДУМАЙ
- Как определить, какое из двух заданных двоичных чисел больше?
А как понять, что они равны? - Как получить число, в 2 раза большее заданного двоичного числа?
- Как получить число, в 8 раз большее заданного двоичного числа?
- Как определить, является ли заданное двоичное число нечётным?
- Как получить число, в 4 раза меньшее заданного двоичного числа?
ПРОВЕРЬ СЕБЯ
●1 Как в двоичной системе счисления записы-
вается десятичное число:
а) 41?
б) 232?
в) 941?
●2 Какому десятичному числу соответствует
двоичное число:
а) 10101?
б) 111010?
в) 1001101?
●3 Какой вид в двоичной системе счисления
имеет сумма двоичных чисел:
а) 1101 и 11011?
б) 11110 и 11101?
●4 Чему в двоичной системе счисления равно
произведение двоичных чисел:
а) 1001 и 111?
б) 11011 и 10111?

Заглавное изображение: begemot.ai






