Хотите удивить своих товарищей демонстрацией эффектного трюка? Если да, тогда эта статья для вас!
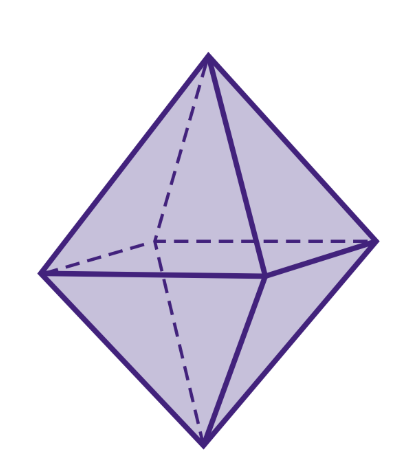
Посмотрите, пожалуйста, на рисунок. На нём изображён октаэдр, один из пяти правильных многогранников. Это тело, имеющее 8 граней (по-гречески «восемь » — οκτώ, откуда и название), в виде равностороннего треугольника, 12 рёбер, 6 вершин (в каждой вершине сходятся 4 ребра).
Октаэдр можно изготовить из бумаги, используя развёртку (см. ниже). Удобно сначала получить один равносторонний треугольник. Вырезав получившийся треугольник, можно затем, используя его как шаблон, нарисовать на плотной бумаге. 8 треугольников, как изображено на развёртке. Участки раз- вёртки, ограниченные пунктирными линиями (они понадобятся при склейке октаэдра), можно потом пририсовать к треугольникам.
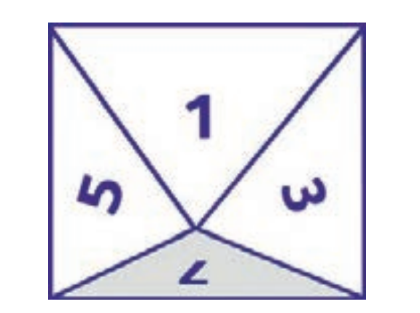
Возникает вопрос — а при чём здесь фокусы? Дело в том, что если на гранях октаэдра написать числа, указанные на развёртке, то его можно использовать для демонстрации любопытного фокуса.
Попросите кого-нибудь задумать любое число от 0 до 7. Положите октаэдр на стол или, держа его в руках, покажите так, чтобы загадавший мог видеть только грани с цифрами 1, 3, 5 и 7. Спросите, видит ли он задуманное число. Если ответ положительный, то запомните про себя число 1. Затем вы переворачиваете октаэдр так, чтобы загадавшему видны только грани с цифрами 2, 3, 6 и 7, и снова задаёте тот же вопрос. Если он ответит положительно, то запомните про себя число 2.
В третий (и последний) раз вы повторяете свой вопрос, повернув октаэдр так, чтобы загадавший мог видеть только грани с цифрами 4, 5, 6 и 7. Утвердительный ответ в этом случае оценивается числом 4. Сложив в уме оценки всех трёх ответов, вы получите задуманное число (или 0, если человек, загадавший число, трижды ответит «нет»). Например, если ответы были «нет», «да» и «да», то задумано число 6 (2 + 4), а если «да», «да» и «нет», то 3 (1 + 2). Секрет фокуса заключается в том, что любое число от 1 до 7 можно представить как сумму чисел 1, 2 и 4:
1 = 1
2 = 2
3 = 2 + 1
4 = 4
5 = 4 + 1
6 = 4 + 2
7 = 4 + 2 + 1
Так вот, четыре числа, которые вы показываете в первый раз (1, 3, 5 и 7), «содержат в себе» единицу, во второй раз (2, 3, 6 и 7) — число 2, в третий раз (4, 5, 6 и 7) — число 4.
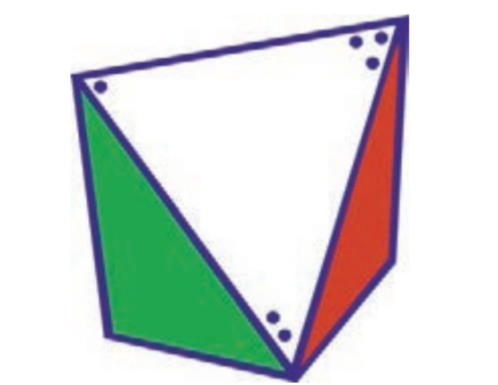
Отвечая на вопросы, человек, загадавший число, невольно подсказывает вам, нужно ли учитывать 1, 2 или 4 в искомой сумме. Чтобы было легче отыскать нужные при демонстрации фокуса положения октаэдра, можно как-нибудь пометить три вершины, которые должны быть обращены к вам, когда вы показываете октаэдр зрителям. Например, можно в качестве меток использовать одну, две и три точки:

Одну точку следует поставить у вер- шины, которая принадлежит граням с числами 0, 2, 4 и 8, две точки — у верши- ны с числами 0, 1, 4 и 5, три — там, где 0, 1, 2 и 3. При первом показе к вам должна быть обращена вершина с одной точкой, при втором — с двумя, при третьем — с тремя. Можно не отмечать числа или точки на гранях, а окрасить грани октаэдра в разные цвета и отгадывать задуманный цвет. Для этого вы должны каждому из чисел от 0 до 7 сопоставить один из восьми цветов и использованные цвета показать зрителям, предложив им выбрать и запомнить любой. Вы потом этот цвет назовёте. Удобно грань с номером 0 сделать белой, а для остальных использовать цвета радуги (кроме фиолетового) и чёрный:
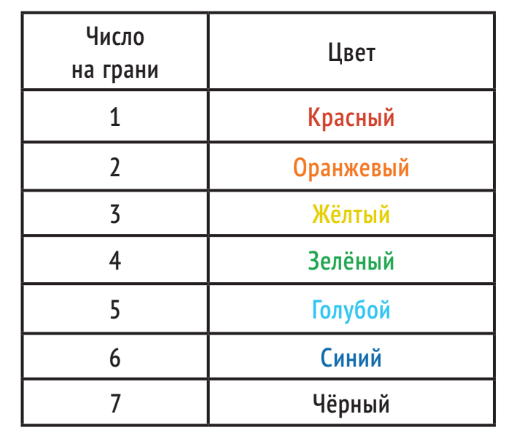
Конечно, при этом вам придётся запомнить эти цвета и числа.
При демонстрации фокуса теперь нужно трижды показывать зрителю октаэдр и спрашивать, видит ли он «свой» цвет. В первый раз вы показываете ему красную, жёлтую, голубую и чёрную грани, во второй — оранжевую, жёлтую, синюю и чёрную, в третий — зелёную, голубую, синюю и чёрную.

По полученной после ответов сумме (как и ранее) вы сможете на- звать загаданный цвет. Например, если ответы были: «да», «нет» и «да», то это голубой (номер этого цвета равен 5), а если «нет», «да» и «нет» — то оран- жевый (2). В таком варианте фокуса для оты- скания нужного положения октаэдра также можно пометить три соответствующие вершины:
Конечно, перед демонстрацией фокусов товарищам надо потренироваться с кем-нибудь дома… Успехов!






