Фигуры, о которых мы поведём речь, представляют собой оптическую иллюзию. В основе зрительного вос- приятия таких фигур лежит визуальное противоречие: кажущаяся проекция трёх- мерного объекта содержит в себе геометрически парадоксальное соединение элементов. Однако не совсем правильно называть такие фигуры невозможными, хотя часто под таким терми- ном они упоминаются в литературе. У большинства из них существует предметное воплощение.
ТРЕУГОЛЬНИК ПЕНРОУЗА
Эту фигуру создал в 1934 году шведский художник Оскар Рутерсвард, и первоначально она состояла из кубиков. Популярность же она приобрела в 1958-м, после статьи о парадоксальных фигурах в «Британском журнале психологии», которую написали английский психиатр Лайонел Пенроуз и его сын, математик Роджер Пенроуз — между прочим, лауреат Нобелевской премии по физике 2020 года. В статье аномальный треугольник был изображён в виде трёх балок, соединённых друг с другом. Пенроузы обобщили несколько парадоксальных фигур, сформулировав единый принцип их создания.

БЕСКОНЕЧНАЯ ЛЕСТНИЦА ПЕНРОУЗА
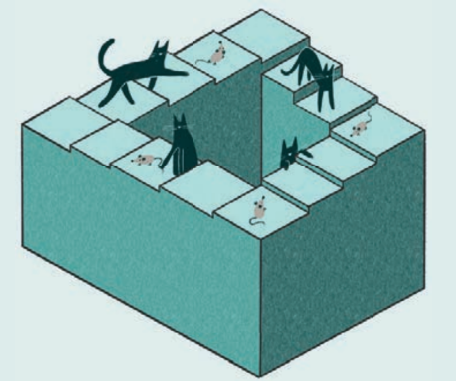
Эта фигура была также разработана Оскаром Рутерсвардом и снискала себе популярность благодаря вышеупомянутой публикации Пенроузов. По ней в одном направлении можно бесконечно подниматься, а в обратном — постоянно спускаться. При этом после завершения визуального маршрута человек окажется в той же точке, с которой начал.
НЕВОЗМОЖНЫЙ ТРЕЗУБЕЦ
Известен также как пойут, бливет или дьявольские вилы. Иллюзия создаёт впечатление, что три цилиндрических стержня превращаются в два бруска. Всматриваясь в верхнюю часть фигуры, наблюдатель видит три стержня. Когда он фиксирует взгляд на нижней части, он видит П-образную фигуру или скобу. Только сфокусировавшись на центре или медленно сколь- зя взглядом по фигуре, он понимает, что видит «невозможную фигуру»

КУБ НЕККЕРА
Фигура стала известна в 1832 году благодаря швейцарскому кристаллографу Луису Неккеру. Зритель воспринимает это изображение неоднозначно: голубая грань словно находится то на переднем, то на заднем плане. Интересно, что куб Неккера иногда используется для проверки компьютерной модели человеческой системы восприятия.

Если подобный эффект неоднозначного восприятия куба повторяется в алгоритмических машинных системах, то он справедливо может быть ассоциирован с переключением между двумя состояниями активности нейронной сети головного мозга. Тем самым формально подтвердится, что машина достигает целостного представления образа тем же способом, что и человек.
С парадоксальными фигурами связано направление в искусстве, названное импоссибилизм или имп-арт (от англ. impossible — невозможный и art — искусство). Один из ярких представителей этого направления — нидерландский художник Мауриц Эшер (1898–1972). Находясь под впечатлением от статьи Пенроузов, он создал несколько литографий с невозможными фигурами. Наиболее популярные из них — «Относительность» и «Водопад». Примечательно, что Эшер в письме к сыну Артуру 24 января 1960 года упоминал статью Пенроузов тоже в своего рода «па- радоксальном» контексте: «Я открыл данный принцип в статье, которую мне прислали, и в которой я сам назван как создатель различных невозможных объектов».
Дело в том, что художник тогда работал над новой картиной, на которой были изображены лестничные пролёты, которые воспринимались восходящими или спускающимися в зависимости от наблюдателя. Несколько фигурок движутся по лестницам в обоих направлениях. Некоторые идут постоянно наверх, а другие бесконечно спускаются. Значительный вклад в понимание предметной реализации невозможных фигур внёс советский и российский художник Вячеслав Колейчукэ. Он создал модель треугольника Пенроуза из дерева: скульптура состоит из искажённых эле- ментов, которые превращаются в прямые линии при взгляде на фигуру с определённого ракурса.

КАК РИСОВАТЬ ТРЕУГОЛЬНИК ПЕНРОУЗА?
Вы тоже можете получить на бумаге невозможную фигуру:
- Нарисуйте треугольник.
- Проведите из каждого угла треугольника отрезки, соблюдая
направление сторон. - Начертите линии, параллельные сторонам треугольника.
- Продолжите свободные концы линий отрезками под углом
45 ° к этим линиям. - Проведите три линии, замыкающие внешний контур фигуры.\

Прежде всего, тема парадоксальных фигур имеет отно- шение к психологии, в частности, к психологии зрительного восприятия человека. Напомним, что отец и сын Пенроузы опубликовали свою знаменитую статью именно в «Британском журнале психологии». Впоследствии эта тема всесторонне исследовалась в ключе психологии. Представляют «невозможные фигуры» интерес и для математиков. Парадоксальные объекты завораживают надолго. Мы сле- дуем взглядом за линиями их построения, за образующими их поверхностями, пытаясь выяснить, где же та «хитрость», которая заставляет реальное принимать за невозможное, а невозможное за реальное. Точно так же наше сознание способно отыскивать ключи к множеству других предметов и явлений, открывая нам перспективы новых удивительных открытий.





