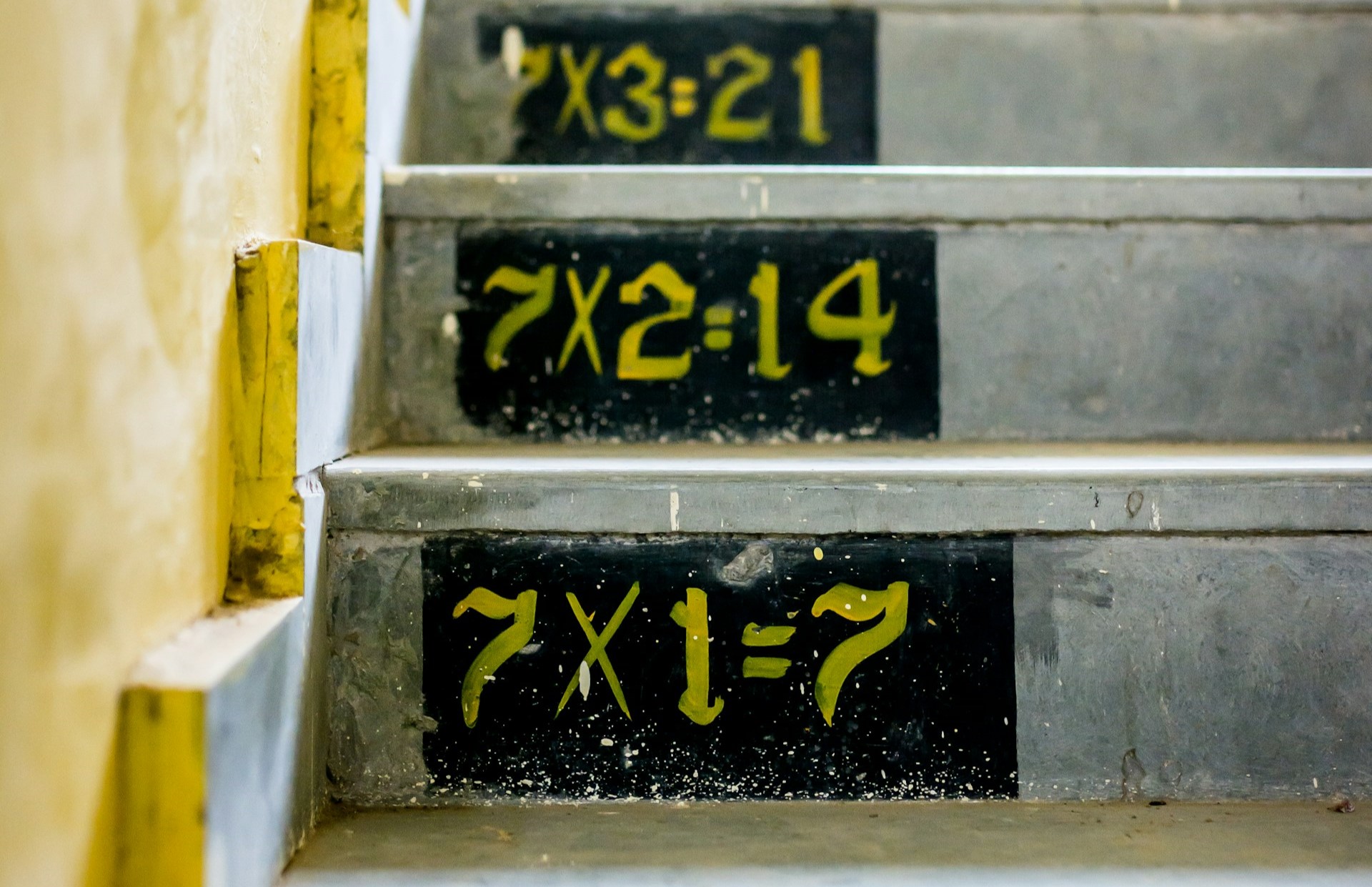Бытует мнение, что математика — исключительно абстрактная наука, которая нужна только в школе. В повседневной жизни, мол, достаточно знать только арифметику — чтобы деньги считать. Взять хотя бы такой раздел математики, как комбинаторика. На ней в школьной программе даже не особо останавливаются — так, гимнастика для ума. А ведь комбинаторика встречается повсюду: от анализа популярных игр до создания лекарств.
ДВА ПРАВИЛА КОМБИНАТОРИКИ
Начнём с хороших новостей: в комбинаторике всего два ключевых правила, которые надо знать. Если вы их поймёте, то поймёте всю комбинаторику. Плохая новость в том, что понять эти правила не так просто.
ПРАВИЛО СУММЫ
Количество вариантов, которыми мы выбираем один объект из двух множеств, равно суммарному количеству объектов в этих множествах. Рассмотрим пример. Если в классе учится 6 девочек и 4 мальчика, то существует 6 + 4 = 10 способов выбрать одного ученика. А если речь идёт о столах или стульях? Действуем точно так же — здесь всё просто. Но иногда требуется выбрать не один объект, а пару: по элементу из каждого множества (в данном случае их два). В этом случае работает правило произведения.
ПРАВИЛО ПРОИЗВЕДЕНИЯ
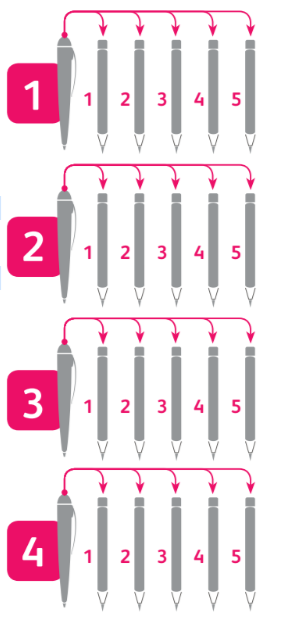
Количество вариантов для выбора пары объектов из двух множеств (первый объект из первого множества, второй — из второго) равно произведению количеств элементов в этих множествах. Опять приведём пример. Допустим, у вас 4 ручки и 5 карандашей. Сколько разных парных комплектов вы сможете собрать?
Для первой ручки 5 вариантов, для второй — тоже 5, для третьей и для четвёртой — снова по 5. Значит, всего вариантов будет 4 × 5 = 20. Это правило работает не только для двух множеств. Если у вас есть ещё и 3 фломастера, то собрать комплект «ручка-карандаш-фломастер» можно 3 × 4 × 5 = 60 способами. Доказывается это аналогично: для каждого из 20 вариантов выбора пары «ручка-карандаш» есть 3 варианта выбора фломастера. Ну а дальше вы уже знаете, что делать.
Сколько комплектов можно собрать из 4 ручек и 5 карандашей? Ответ: 4 × 5 = 20 комплектов
Попробуем разобраться, как отличить одно правило от другого. Допустим, в финале турнира по Dota 2 играли 2 команды по 5 человек, и требуется выбрать одного из финалистов, которого назовут MVP-турнира. Сколько есть способов это сделать? Ответ — 10. Работает правило суммы, так как мы выбираем один элемент из двух. А если нужно выбрать по одному игроку из каждой команды и наградить их как лучших в своих коллективах, сколько вариантов выбрать такую пару? Ответ — 25. Здесь мы применяем правило произведения — ведь нужно выбрать не один объект, а пару! Разобрались? Тогда переходим к примерам из жизни.
МАГИЯ НОЛИКОВ И ЕДИНИЧЕК
Информация в компьютере хранится в двоичном коде, то есть записана нулями и единицами. Одна ячейка памяти, она же бит, содержит либо 0, либо 1. И вот вопрос: сколько битов понадобится, чтобы закодировать, например, латинский алфавит из 26 букв? Предполагается, что каждую букву мы кодируем одинаковым количеством битов, и очевидно, что это количество должно быть минимальным, чтобы буквы занимали меньше места в памяти. Не пугайтесь, если вы не видите решение сразу. В таких случаях надо немного порассуждать или попробовать перебрать простые ответы. Что, если если бит всего один? Значит, в нём может быть записан либо 0, либо 1. То есть только два варианта, или всего две буквы. Маловато. Допустим, битов будет два, или две ячейки. Сколько разных вариантов двузначного числа можно составить из нулей и единиц? Каждую ячейку можно представить как множество, в котором есть либо 0 либо 1.
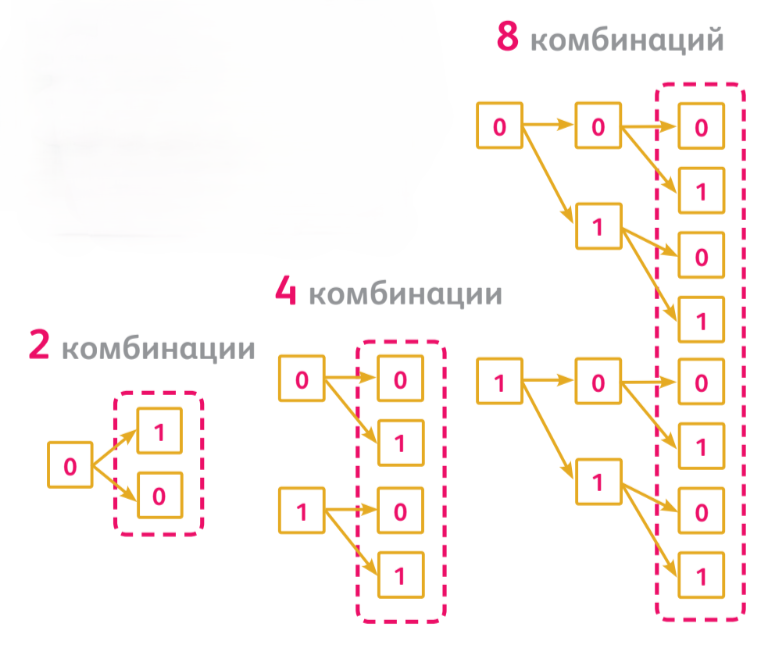
Тогда наша задача — выбрать два элемента из двух множеств. Это и есть правило произведения. Получаем четыре варианта. Тоже мало. По аналогии, беря три бита, имеем три ячейки для заполнения. А значит, по всё тому же правилу произведения у нас будет 2 × 2 × 2 = 8 различных вариантов составить комбинацию из нулей и единиц. Соответственно, четыре бита дадут 2 × 2 × 2 × 2 =16 вариантов, а пять — 32. Это нам уже подходит, так как 32 больше, чем 26. Значит, для кодирования латинского алфавита потребуется как минимум пять битов. И пришли мы к ответу с помощью правила произведения.
В МИРЕ УНИКАЛЬНЫХ НОМЕРОВ
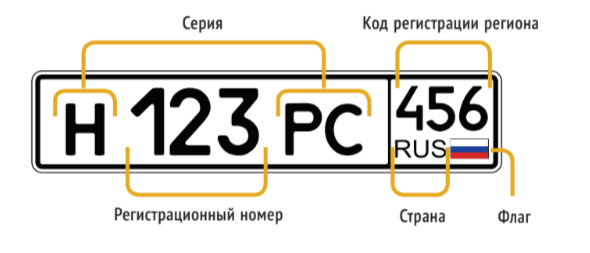
14 августа 1893 года Франция стала первой страной в мире, которая ввела регистрационный знак на транспорт. Позже это сделают практически все страны мира. Регистрационный знак — это уникальная комбинация букв и цифр, он нужен для однозначного определения владельца и транспорта. За почти полтора века количество автомобилей в мире превысило миллиард единиц, и каждому требуется свой уникальный номер. Как решается эта проблема сегодня? Рассмотрим автомобильный номер из трёх цифр и букв — такой формат принят в таких странах, как Канада, Ботсвана, Швеция, Казахстан и Россия. Оговоримся сразу, что мы не берем в расчёт код региона, о нём поговорим отдельно. Прежде всего отметим, что буквы могут быть только латинскими.
Соответственно, для каждой цифры есть 10, а для каждой буквы — 26 вариантов. Сколько же уникальных номеров можно составить? Мы должны выбрать одну комбинацию из трёх множеств по десять цифр и трёх множеств по двадцать шесть букв. То есть мы должны применить правило произведения: 10 × 10 × 10 × 26 × 26 × 26 = 17 576 000
10 × 10 × 10 × 26 × 26 × 26 = 17 576 000
Много это или мало? Например, в Канаде проживает 35 млн человек, или в среднем по около 2,7 млн человек в 13 провинциях. Даже если у каждого жителя, включая детей, будет по автомобилю, всем достанется уникальный номер. В действительности 38 % населения, или более 13 млн человек, проживает в провинции Онтарио. Как видно, и для неё этого числа было бы достаточно. Но в 1997 году провинция решила перейти на формат четыре буквы и три цифры, тем самым ещё расширив диапазон номеров. Аналогично жители распределились и в России — наиболее плотно населены Москва и Московская область. Как мы говорили ранее, к номеру из трёх цифр приписывают код региона, у густонаселённых регионов таких кодов может быть несколько. Вы можете сами подсчитать, сколько цифр должно быть в телефонном номере в вашем городе, чтобы всем хватило номеров! Работает правило произведения в чистом виде.
СЛОЖНЫЕ ПАРОЛИ И ПРОСТЫЕ
В любом современном мобильном телефоне есть парольная защита. Самая простая из которых — четыре цифры пинкода (от 0 до 9). Зная правило умножения, вы можете посчитать, сколько разных вариантов нужно перебрать злоумышленникам, чтобы подобрать пароль: 10 × 10 × 10 × 10 = 10 000.
Как вы думаете, это внушительное количество? Сегодня в телефоны встроена и защита от перебора — после нескольких неудачных попыток ввода пароля ваше устройство блокируется. Но если вы думаете, что четырёхзначного пина достаточно, у нас для вас плохие новости. Британская компания по компьютерной безопасности MDSec продемонстрировала устройство, которое максимум за 111 часов сможет подобрать любой четырёхзначный пароль. Хитрость в том, что устройство вводит пароль и ожидает 40 секунд — так оно обходит систему защиты. В итоге оно может взломать устройство за 4,6 дня непрерывной работы.
Насколько изменилась бы ситуация, если бы можно было использовать и буквы? Сперва применим правило суммы и определим, сколько существует способов выбрать один объект из двух множеств: 10 цифр + 26 букв = 36 вариантов. Теперь применим правило умножения и определим количество способов выбрать пароль из четырёх множеств по 36 элементов: 36 × 36 × 36 × 36 = 1 679 616 вариантов. На перебор этих вариантов потребуется: 40 × 1 679 616 = 67 184 640 секунд, или 777 дней. В качестве самостоятельной работы попробуйте посчитать количество вариантов пароля, который соответствует современным стандартам безопасности:
- Длина пароля не менее 8 символов.
- Обязательное использование заглавных букв (А–Z)
- Обязательное использование строчных букв (а–z)
- Обязательное использование цифр (0–9)
- Обязательное использование специальных символов
- (~`!@#$%^&*()+=_-{}[]|:;»’?/<>,.)
И самое главное: пытаясь обезопасить себя, не забудьте пароль.
ЗАНИМАТЕЛЬНЫЕ ФЛАГИ


Порядка 30 % всех существующих национальных флагов похожи — это три полосы двух или трёх цветов. Как правило эти цвета символизируют ценности этой
страны или её историю. Например, цвета
государственного флага Германии — чёрный, красный и золотой.
Более того, почти у всех стран цвета на флагах олицетворяют схожие понятия. Самые распространённые — чёрный, красный, голубой, зелёный, белый и жёлтый. Давайте представим, сколько трёхполосных флагов можно было бы сделать из комбинации 6 цветов. Хватило бы их на 252 государства? Считаем: в качестве первой полосы мы можем использовать любую из шести. В качестве второй… А вот тут аккуратнее: логично предположить, что вторая полоса должна по цвету отличаться от первой, так что вариантов уже 5. Для третьей полосы — 4, если мы не хотим, чтобы цвета повторялись. Либо 6 — если согласны на совпадение первой и третьей (как на флаге Австрии или Аргентины). Итого: 6 × 5 × 4 = 120 вариантов.
Напомним, мы применили правило произведения, так как выбираем тройку объектов из трёх множеств, а не один объект. К счастью вексиллологов, занимающихся изучением флагов, знамён, штандартов и вымпелов, стандартизация всех флагов невозможна. И мы привели тому строгое математическое доказательство. Мы привели примеры использования двух простых, но важных правил, которые лежат в основе комбинаторики, занимающейся подсчётом вариантов и комбинаций. В свою очередь, варианты и комбинации лежат в основе расчёта, например, вероятности событий — от выигрыша в играх до кризисов в экономике. Ну что, не такая уж комбинаторика и бесполезная?
Заглавное изображение: Unsplash