Каков средний возраст современного кинозрителя (величина А), какой самый популярный фильм 2016 года (величина В) и чему равен максимальный возраст младшей половины аудитории фильма «Кунг-фу Панда»? (величина С).
Такая информация всегда необходима кинокомпаниям, может быть полезна владельцам кинозалов и даже может заинтересовать кинозрителей. Знаете, что общего у этих разных, на первый взгляд, величин? Величины А, В и С являются серединами. О них мы и поговорим.
Начнём с того, что все эти величины — А,B и С — можно определить только тогда, если у вас есть данные. В первом случае, это количество людей, посетивших кинотеатры и их возраст. Во втором — список фильмов 2016 года и количество билетов, проданных на каждый фильм. И в последнем случае — это количество людей, посмотревших фильм «Кунг-фу Панда» с указанием их возраста. Проанализировав и обработав имеющиеся данные, мы можем найти значение величин А,В и С.
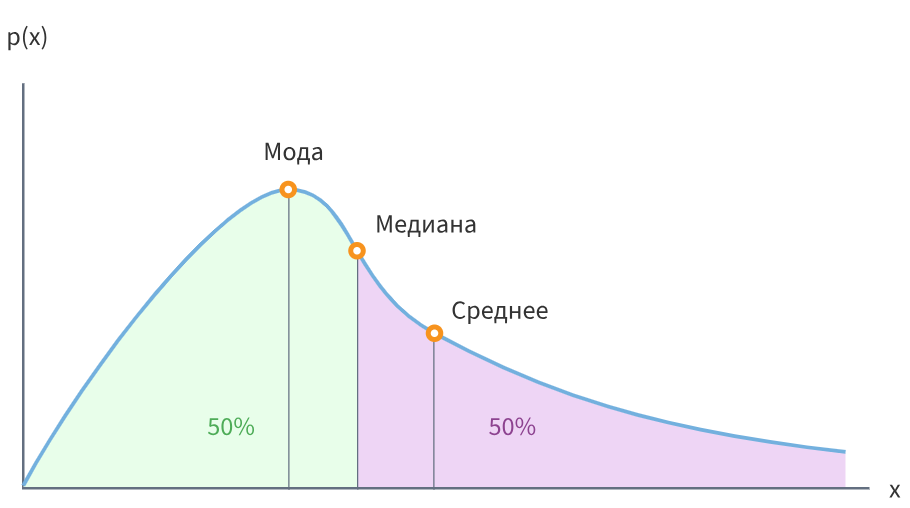
Каждая из названных величин является «центром» или «серединой» этих данных. В математической статистике их называют средним арифметическим (А), модой (В) и медианой (С).Эти величины несут в себе определённую ин-формацию об имеющихся данных и могут быть полезными в повседневной жизни. Чтобы было понятно, объясним это на примере.

Пример
Среди школьников четвёртых классов провели годовую контрольную по математике. Класс, который покажет наилучший результат, наградят поездкой в летний лагерь. В каждом классе по 30 учеников. Победителя решили определить, вычислив среднюю арифметическую оценку по каждому классу.
Самый распространённый вид средней величины — средняя арифметическая. Как она считается, знают все: нужно сложить все слагаемые и сумму разделить на количество этих слагаемых.

Наивысший результат показал 4 «В» класс. «Ура! Мы едем в лагерь!» — обрадовались ученики 4 «В» класса. Но тут возмутились ученики 4 «А» и 4«Б» классов: «Мы должны поехать в летний лагерь, у нас больше «пятёрок»! Директор был в замешательстве: «Что делать?». Тогда учитель математики предложил посчитать моду.
Мода — это наиболее часто встречающееся значение в данных. Мода применяется, например, на обувных фабриках, при определении самого «ходового» размера обуви, то есть пользующегося наибольшим спросом у покупателей. В самом деле, не будут же производители обуви ориентироваться на средний размер обуви и шить всю обувь среднего размера.
По этому показателю лучшими оказались 4 «А» и 4 «Б» классы — у них самой «модной» оценкой оказалась «пятёрка», тогда как в 4 «В» «модная» оценка была ниже — это была «четвёрка». Директор был озадачен: «Получается, что нужно поощрить сразу два класса, но количество мест в лагере ограничено!».

Тогда ученики 4 «А» начали говорить, что они всё равно лучше, потому что у них «пятёрок» больше, чему 4 «Б». В ответ на это 4 «Б» возмущённо сказал: «Зато у нас троек меньше, чем у вас. Должны ехать мы!» Директор школы опять оказался в затруднительном положении. Но неунывающий учитель математики предложил рассчитать медиану.
Медиана — это некая отметка, делящая ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Она расположена в центре ранжированного ряда. То есть половина исходных данных по своему значению меньше этой отметки, а половина — больше.
Вот как нужно находить её в наборе данных.
- Расположите числа по возрастающей.
- Если в наборе данных насчитывается нечётное количеством чисел, выберите то, которое расположено точно посередине. Это и есть медиана.
- Если в наборе данных чётное количество чисел, найдите среднее значение двух чисел, которые расположены посередине, это и будет медианой.

«Ну теперь точно поедем мы!» — радовался 4 «А», наша медиана «4,5», а у 4«Б» и 4 «В» — «четвёрка». Это значит, что половина нашего класса получила отметку выше, чем 4,5 (то есть только пятёрки), а у других классов эта же половина получила отметку выше «4» (то есть не только «пятёрки», но и «четвёрки»). Но тут подал голос 4 «В», до этого невступавший в спор: «А у нас вообще “троек” нет, значит, у нас нет отстающих, и это немаловажный показатель!». «А ведь они тоже правы»,— подумал директор и ещё больше загрустил.
Средняя величина — это усреднённый показатель, который уничтожает индивидуальные различия и даёт обобщающую характеристику показателю. Бывают случаи, когда средняя арифметическая не совсем подходит для решения поставленной за-дачи и даже может ввести в заблуждение. Тогда используются другие средние величины — мода и медиана.
Мода и медиана — важные показатели, они отражают структуру данных и, в отличие от средней арифметической, не погашают индивидуальных различий изучаемого показателя. Поэтому они являются дополнительными и очень важными характеристиками и на практике часто используются вместо сред-ней арифметической либо наряду с ней.
А какой класс отправили бы вы, будь вы на месте директора?