Вы замечали, что споры часто бывают неконструктивными, а побеждает тот, кто громче крикнул или резче высказался? Но если дискутировать по законам логики, любой спор разрешается довольно просто. В математике этот приём доведён до совершенства.
Начнём с простого. Мы часто пытаемся донести до собеседника некую мысль, но сделать это бывает непросто. Тогда мы прибегаем к примерам. Допустим: «Женщины способны играть в шахматы ничуть не хуже мужчин. Например, венгерская шахматистка Юдит Полнар выигрывала у ведущих гроссмейстеров и долгое время была в первой десятке мирового рейтинга». Если бы не конкретный пример, вы могли просто ответить: «Нет, я считаю иначе». Но согласитесь, с примером тезис стал убедительнее?
Теперь рассмотрим другой пример: вам говорят, что все футболисты блондины. Как доказать собеседнику, что он неправ? Самое разумное — привести обратный, или контрпример. Почему? Потому что он один перевесит тысячи примеров «за»! Ваш собеседник может десятками перечислять блондинов, но вы поставите точку в споре, вспомнив, например, Леонеля Месси. В решении математических задач контрпримеры занимают особое место. Не верите? Мы докажем обратное.

ЗАДАНИЕ 1. СУЩЕСТВУЕТ ЛИ ЧИСЛО, КОТОРОЕ ЗАПИСЫВАЕТСЯ ОДНИМ И ТЕМ ЖЕ КОЛИЧЕСТВОМ ЦИФР И БУКВ?
Разумеется, всё зависит от языка, на кото- ром мы говорим. Но как решать задачу? Неужели проверять все числа подряд? Так можно и до миллиона дойти… Стойте-ка! В слове «миллион» ровно 7 букв, и для его записи требуется 7 цифр: единица и шесть нулей. Обратите внимание: чтобы решить эту задачу, нужен всего один пример. При этом одного опровергающего примера недостаточно! Допустим, 10 не подходит, ну и что? Из этого вовсе не следует, что чисел, которые записываются одним и тем же количеством цифр и букв, не существует. Вопрос «А как, собственно, найти искомое число?» оставим без ответа. Нам важно, что, если требуется записать решение, оно будет крайне лаконичным: «Да. Например, миллион». Построение контр- примера — обычный способ опровержения гипотез. А как сделать из этой задачи гипотезу, думаем, вы разберётесь.
ЗАДАНИЕ 2. МОЖЕТ ЛИ СУММА А) ДВУХ, Б) ТРЁХ, В) БОЛЕЕ ЧЕМ СТА ЦЕЛЫХ ЧИСЕЛ БЫТЬ РАВНА ИХ ПРОИЗВЕДЕНИЮ?
Начнём с первого пункта. Придумать пример довольно легко: скажем, 0 и 0. Заметьте, всё, что не запрещено, разрешено. Так что числа могут быть нулями — хоть все. Это рассуждение применимо и для остальных пунктов, поэтому давайте решим чуть более сложную задачу. Что, если бы числа в условии были натуральными, а не целыми? Первый пункт всё ещё не составляет труда — многие из вас уже дали ответ: 2 и 2. Интересно, что это единственный пример, но доказательства от нас не требуют.
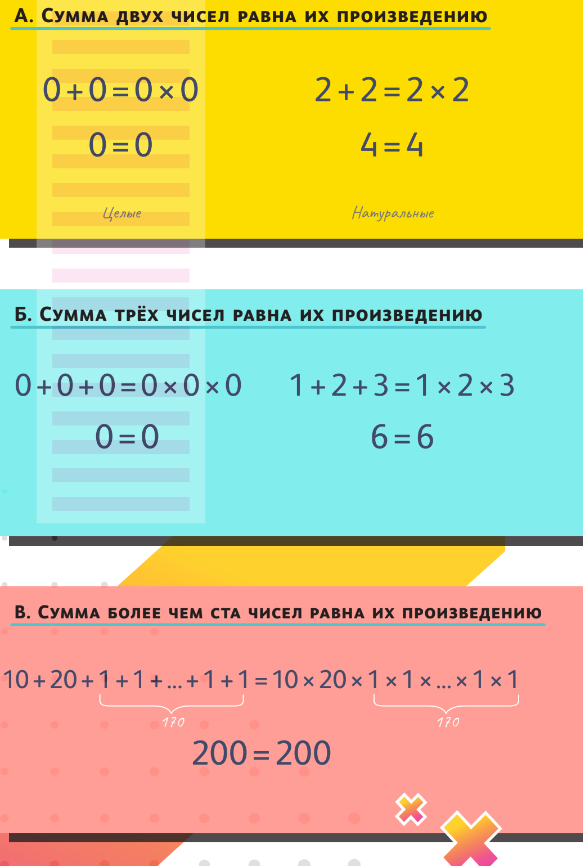
Что касается второго пункта, тут тоже несложно догадаться: «1, 2, 3». Отсюда, кстати, важный совет: когда подбираете примеры, начинайте с простых. В случае чисел — с самых маленьких. Переходим к третьему пункту. Прежде всего обратим внимание на такой небезынтересный факт: обычно произведение чисел намного больше их суммы. Действительно, если мы добавляем к на- бору чисел ещё одно, то сумма увеличивается на это число, а произведение растёт в это число раз. Потому оно и больше суммы. Впрочем, есть исключение: если числом, которое мы прибавим или на которое умножим, будет единица, то произведение не изменится вовсе, а сумма увеличится на 1. Это и есть ключ к решению.
Рассмотрим, например, числа 10 и 20. Их сумма равна 30, а произведение 200. И если до- писать к ним 170 единиц, то в полученном наборе и сумма, и произведение будут равны 200, что и требовалось доказать. Обратите внимание, как мы действовали, решая последнюю задачку. Мы осознали, что в ней удивляет (произведение обычно больше суммы, а тут совпадает); поняли, как произведение может не вырасти; построили пример. Числа 10 и 20 кажутся взятыми с потолка, но подошли бы любые другие. Ну, или почти любые: если мы возьмём 10 и 10, то для уравнивания суммы (20) и произведения (100) потребуются 80 единиц, а значит, всего чисел будет меньше 100.
ЗАДАНИЕ 3. МАДРИДСКИЙ «РЕАЛ» ОДЕРЖАЛ В ЧЕМПИОНАТЕ ИСПАНИИ ПО ФУТБОЛУ, ГДЕ УЧАСТВУЮТ 20 КОМАНД, БОЛЬШЕ ВСЕХ ПОБЕД. МОГ ЛИ ОН ПРИ ЭТОМ ЗАНЯТЬ ПОСЛЕДНЕЕ МЕСТО?
Как и в прошлом задании (но здесь ещё больше), вопрос поначалу кажется абсурдным. Если команда выигрывала чаще остальных, как она может быть последней, то есть набрать наименьшее количество очков? Иначе говоря, как другие команды могли набрать больше очков, если побед (очков за победы) у них меньше? Единственный логичный ответ: за счёт ничьих. Эта гипотеза поможет построить пример. Для начала предположим, что «Реал» одержал не очень много побед. Одну? Хорошо, но тогда у остальных будет ноль побед, ведь по условию задачи их меньше, чем у «Реала». А значит, с «Реалом» все эти команды сыграли вничью, что даёт «Реалу» много очков за ничьи. Не годится.
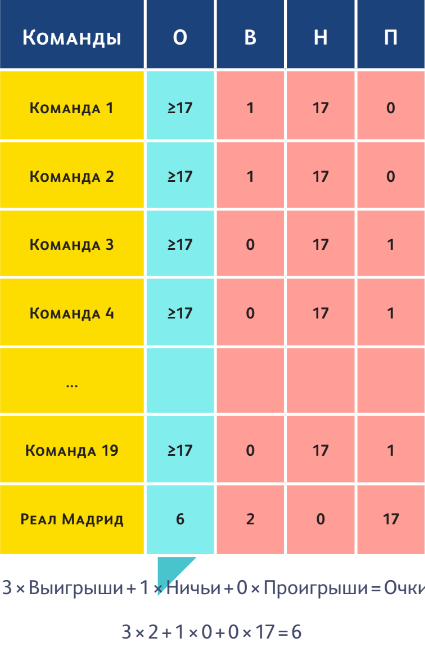
Пусть «Реал» выиграл два раза, тогда остальные могли одер- жать по одной победе — над «Реалом»,— все, кроме двух про- игравших ему команд. Матчи же между собой они, допустим, завершили вничью. В этом случае у «Реала» будет 6 очков, а у остальных команд как минимум по 17 благодаря ничьим. Вообще говоря, чемпионат Испании проводится в два круга — каждый играет с каждым по два матча, так что отставание «Реала» будет ещё большим. Единственный недостаток указанного примера — что «Барселона» не заняла чистое первое место, но мы-то знаем…
ЗАДАНИЕ 4. МОЖЕТ ЛИ ПРОИЗВЕДЕНИЕ ЦИФР ЧЕТЫРЁХЗНАЧНОГО ЧИСЛА БЫТЬ РАВНЫМ А) 12, Б) 22?
В первом пункте хватит одного примера: допустим, 2231. Из чего это следует? Мы разложили 12 на множители, получили 2, 2 и 3, после чего догадались, что число должно быть четырёхзначным, так что надо дописать ещё одну цифру, не изменив произведения. Конечно, это единица. Впрочем, существуют и другие примеры: 2611, 4131 и т. д. Во втором пункте тоже достаточно одного примера… Только он что-то не приводится. Во- обще, это самая большая проблема подобных задач: мы не можем быть уверены, что такой пример вообще существует! Можно потратить кучу времени на поиски того, чего нет. Поэтому наш совет: если не уверены в ответе на вопрос «можно ли», попробуйте искать примеры «за» и «против».

В данной задаче искомого числа действительно нет. Но то, что мы не придумали пример, не доказательство: мало ли, может, мы просто его не нашли. Доказательство же такое: 22 — это произведение 2 и 11, а 11 — простое число. Это значит, что произведение цифр искомого числа делится на 11, а тогда одна из цифр должна делиться на 11, чего не бывает, так как самая большая цифра — 9. Точнее, бывает, если одна из цифр равна 0, но в этом случае произведение будет 0, а не 22.
Итак, мы доказали, что 22 получить невозможно. Но ещё раз повторим: то, что мы не смогли привести пример, отнюдь не доказывает отсутствие решения. Между прочим, небезызвестная теорема Ферма примерно в этом и состояла: великий математик сказал, что не существует таких целых x, y, z, а также натурального n > 2, для которых xn + yn = zn. И долгие годы никто не мог придумать контрпример, однако это не доказывало справедливость теоремы Ферма.
ЗАДАНИЕ 5. СУЩЕСТВУЮТ ЛИ ТАКИЕ ЦЕЛЫЕ X, Y И Z, ЧТО 28X + 30Y + 31Z = 365?
Эту задачу можно решать по-разному. Понятно, что одного примера будет достаточно, вот только как этот пример найти? Давайте рассуждать так. Слева стоят числа, близкие к 30, значит, их надо взять примерно 12 раз, чтобы получить 365. Предположим, что y = 12, x = z = 0. Тогда левая часть будет равна 360. Хорошо, теперь перекинем единицу из у в z. В этом случае мы вычитаем из левой части 30, а прибавляем 31, то есть в итоге добавляем 1. Проделав эту манипуляцию пять раз, получаем искомое решение: x = 0, y = 7, z = 5.
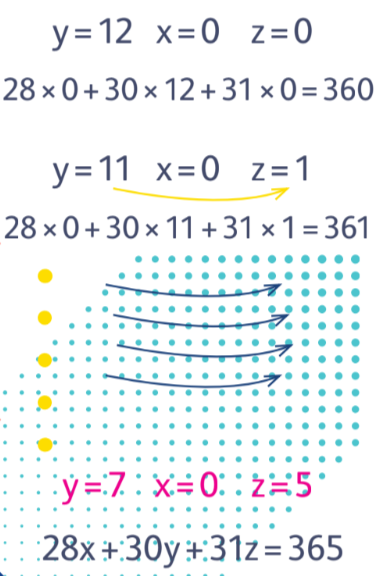
Можно пойти другим путём. Число в правой части равенства оканчивается на 5, значит, и в левой должно быть так же. Понятно, что 30у не влияет на последнюю цифру, то есть получить 5 надо с помощью 28х или 31z. Проще всего, наверное, взять z = 5, тогда 31z = 155. Осталось набрать 210 — это легко сделать, взяв у = 7, что приводит нас к уже найденному решению: x = 0, y = 7, z = 5. Есть, правда, одно «но». Что тут красивого? Задача и задача, копаемся в каких-то уравнениях, что-то как-то подбираем… Давайте посмотрим повнимательнее. Коэффициенты 28, 30 и 31. В правой части — 365.
К чему бы это? Точно, это же количество дней в месяцах и в году! Так что если посчитать, сколько в не високосном году месяцев длиной 28 дней (1), сколько длиной 30 дней (4), а сколько 31 (7), мы придём к весьма элегантному решению: x = 1, y = 4, z = 7. Надеюсь, и вам оно кажется более красивым. Впрочем, от этого предыдущие решения не стали неверными. Подведём итоги. Если в задаче спрашивается, «можно ли», «существует ли» и так далее, ответ «да» достаточно проиллюстрировать всего одним примером. А вот ответ «нет» требует доказательства. Аналогично дело обстоит с контрпримерами.






