Как долго будет длиться карантин? Когда наступит пик заболеваемости? Сколько человек в итоге переболеет коронавирусом? Все учёные ищут ответы на эти вопросы. Мы предлагаем вам самим ответить на них. Поможет математика, а именно — математическое моделирование.

Начнём с определения: математическая модель — это описание какого-либо явления через уравнения. Решая их, мы можем предсказать, как это явление будет себя вести. Но зачем описывать что-то реальное абстрактными уравнениями и тратить силы на их решение? Всё дело в природе описываемых явлений. Например, реальный эксперимент может быть слишком дорого- стоящим или опасным. Либо, как в случае с эпидемией, нам нужны ответы до её начала, чтобы предпринять необходимые меры. Для моделирования вам может быть достаточно клочка бумаги и карандаша, а в случае больших задач в ход идут суперкомпьютеры, но даже такие затраты и усилия многократно окупаются.

МОДЕЛЬ РОСТА НАСЕЛЕНИЯ МИРА

В 1760 году в Великобритании началась Великая индустриальная революция. Менее чем за век она изменила уклад жизни людей, превратив аграрное общество в индустриальное, а новые блага повлияли на мировую демографию. К примеру, население Англии за это короткое время удвоилось. Эти события происходили на глазах английского демографа и экономиста Томаса Мальтуса (1766–1834). По его мнению, такой неконтролируемый рост народонаселения должен был в конце концов привести к голоду на Земле. Но такие прогнозы требовали доказательств, и в 1798 году Мальтус представил простую математическую модель изменения численности людей. За счёт чего меняется численность населения? Во-первых, она растёт за счёт родившихся — поэтому Мальтус ввёл понятие удельной рождаемости γ (выражение γ = 0,07 означает, что на 1000 человек родилось 70 малышей). Во-вторых, она уменьшается из-за смерти, это описывает удельная смертность β (β, равная 0,005, означает, что на 1000 человек умерло 5 человек). Также Мальтус ввёл удельный прирост a = γ − β, т. е. разница между удельной рождаемостью и смертностью. Если a < 0, значит, смертность превышает рождаемость и численность людей будет убывать. При a > 0, соответственно, она возрастает.

Пусть в начале численность населения была N₀. Как она изменится через один, два, три или t лет? Всё просто, надо к исходному количеству людей прибавить родившихся и вычесть умерших, и так из года в год.

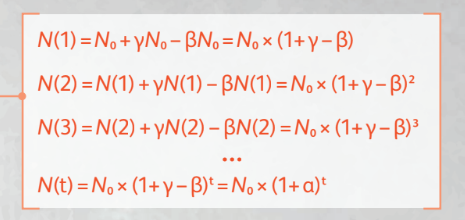
Если перегруппировать эти формулы, получится одно дифференциальное уравнение, которое описывает всю модель Мальтуса. Однако мы не будем пугать вас и представим упрощённую схему уравнения:

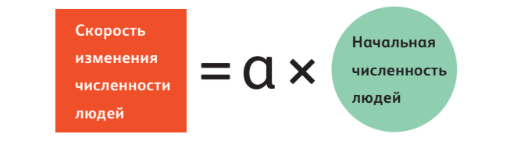
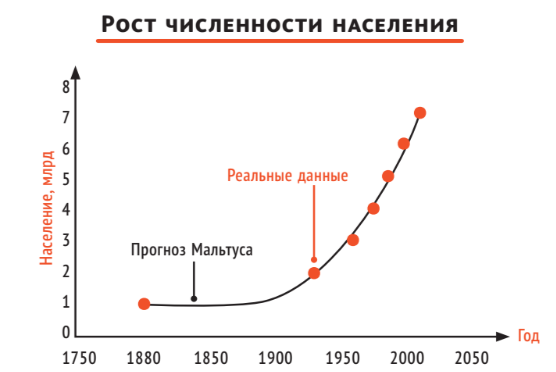
По данным Мальтуса, а было положительным, поэтому население Земли возрастало изо дня в день. Решение модели очень простое и представляет собой показательную функцию от одной переменной. Модель оказалась весьма точной: сравните график Мальтуса с реальным графиком роста численности населения мира. Так Мальтус пришёл к закономерному выводу об экспоненциальном росте численности населения.

Одновременно с этим Мальтус анализировал ресурсы планеты и сделал вывод, что мы способны добывать их в ограниченном количестве. Иначе говоря, потребности человечества растут в геометрической прогрессии (пропорционально числу людей), а количество добываемых ресурсов растёт в арифметической. Значит, наступит момент, когда ресурсов станет недостаточно для удовлетворения наших потребностей и мы окажемся в «мальтузианской ловушке» (в экономике данная теория получила название «мальтузианство»). Американский эволюционный биолог и автор книги «Ружья, микробы и сталь» Джаред Даймонд утверждает, что геноцид в Руанде в 1994 году представляет собой современный пример «мальтузианской ловушки». Перенаселение в бедной аграрной африканской стране стало одной из при- чин массовых кровавых беспорядков.

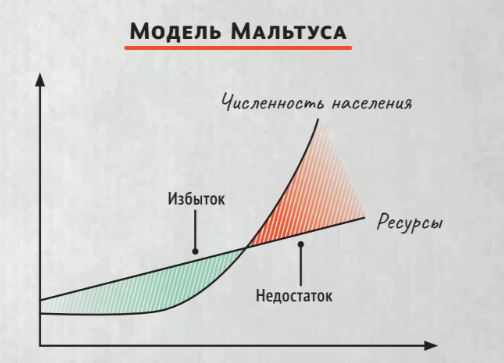
Модель Мальтуса достаточно точно описывает начальную фазу роста населения, но учитывает не все факторы, оказывающие влияние на демографию. Например, чем выше уровень благосостояния общества, тем меньше рождаемость, а применение новых технологий или использование возобновляемых источников энергии может увеличить добычу ресурсов. Но, несмотря на это, у человечества есть повод задуматься над бережным отношением к ресурсам планеты, ведь очевидно, что они конечны.

ЗАКОН ФАРРА

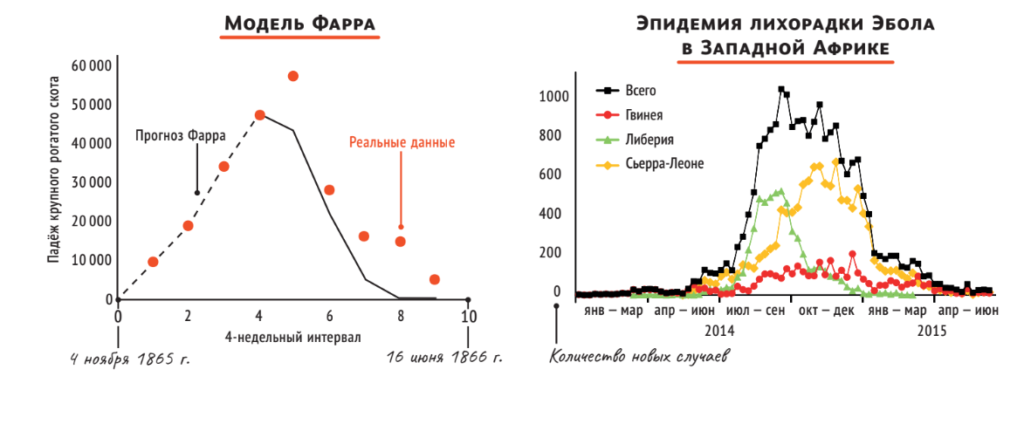
Английский демограф и основатель медицинской статистики Ульям Фарр (1807–1883) исследовал распространение холеры. Но вместо лекарств он вооружился числами. Работая более 40 лет в Главной службе регистрации Соединённого Королевства, он имел доступ ко всевозможным данным со всех уголков страны. Анализируя их, Фарр искал взаимосвязи между профессиями и болезнями, плотностью населения и смертностью, а также закономерность эпидемий. Фарр обнаружил, что эпидемии так же быстро угасают, как и вспыхивают — то есть экспоненциальный рост сменяется таким же экспоненциальным снижением.

В 1865–1866 годах в Англии разразилась эпидемия чумы крупного рогатого скота. Экспоненциальный рост количества заболевшего скота означал, что скоро страна останется без мясного продовольствия. Но Фарр предсказал скорый резкий спад эпидемии после достижения некоторого пика. Что в итоге и произошло. Большинство эпидемий подчиняются закону Фарра, например, взлёт и падение числа больных лихорадкой Эбола в Западной Африке в 2014 году. Однако модель Фарра основывалась на статистических данных и не могла точно предсказать, когда именно наступит спад заболевания. В 1927 году Ульям Кермак и Андерсон Маккендрик разработали модель распространения эпидемий SIR. Модель делит людей на три группы: S(t) — здоровые люди (Susceptible); I(t) — инфицированные люди (Infected); R(t)— «выбывшие» люди (Recovered). К ним относят выздоровевших и умерших.

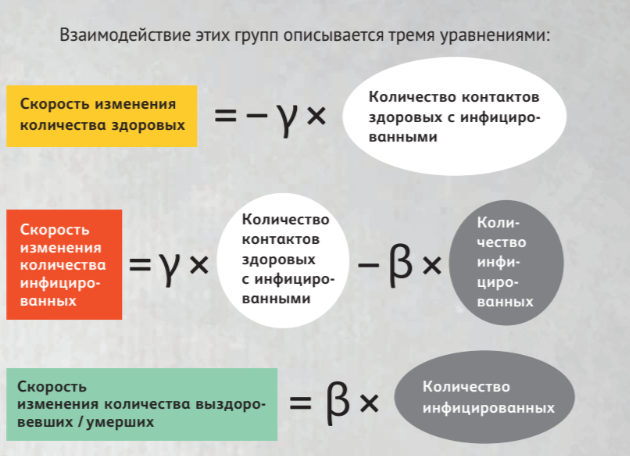
Где γ — вероятность заражения здорового человека, а β — скорость выздоровления/смерти. Обратите внимание, что впервые в модели предлагается использовать наблюдения медиков и особенности каждой болезни. Введём ещё один важный параметр, R₀ — среднее количество людей, которых заразит 1 инфицированный человек (S₀— начальное количество здоровых людей):

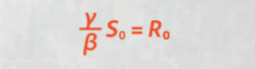
Для обычного сезонного гриппа значение R0 варьируется между 1,5 и 2, тогда как для коронавируса оно составляет от 3 до 4.

ИГРА В ПРЕДСКАЗАТЕЛЯ

Теперь попробуем применить эту модель на практике и ответить на настоящие вопросы. Пусть стало известно, что в городке с населением 101 человек 1 заразился вирусом COVID-19. Вам срочно надо ответить на следующие вопросы: 1) Сколько человек будет болеть единовременно? 2) Когда наступит пик эпидемии? 3) Как снизится заболеваемость, если ввести карантин?

1) Сколько человек будет болеть единовременно?
2) Когда наступит пик эпидемии?
3) Как снизится заболеваемость, если ввести
карантин?

Подставим в формулу известные данные: N = 101, S₀ = 100, I₀ = 1.

Согласно данным по коронавирусу, β = 0,27, R₀ = 3. Зная R0, S₀ и β, мы можем вычислить γ:

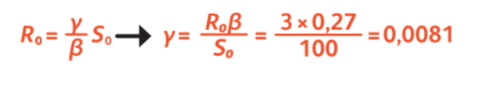
Пропустим математические выкладки и проанализируем график решения:

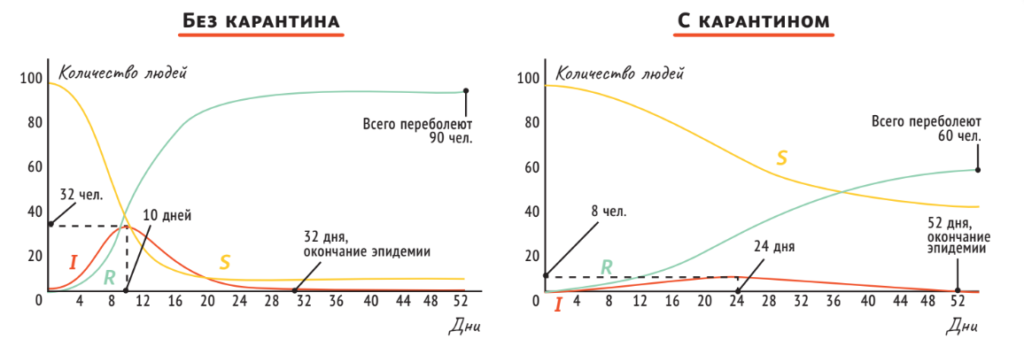
Видно, что максимальное число заболевших будет 32 человека. Этот пик будет достигнут на 10-й день, а спустя 31 день эпидемия должна сойти на нет. Как повлияет на ситуацию ввод карантина? Предположим, что каждый второй житель будет сидеть дома. Тогда коэффициент γ (вероятность заболеть) изменится. Каким образом? Пусть в среднем 1 человек общается с 10 людьми в день. Так как R₀ = 3, это означает, что 1 инфицированный заражает 30 % людей, с которыми общался. Поскольку каждый второй житель остался дома, у заболевшего будет только 5 контактов, значит:

R₀ = 0,3 × 5 = 1,5

Тогда:

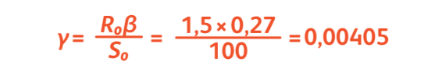
Главный вывод — число заболевших не превысит 8 человек, вместо 32, т. е. заболеваемость снизится на 75 %. Но время эпидемии почти удвоится, и всё это время мы должны будем поддерживать режим карантина. Математические модели стали неотъемлемым инструментом для принятия решений: они позволя- ют управлять неопределённостью и предсказать вероятные сценарии развития событий. Ну а мы ещё раз напоминаем, что очень важно сейчас оставаться дома, мыть чаще руки. Потому что таким образом вы снижаете вероятность заболеть, а значит, R0 будет стремительно уменьшаться и скоро коронавирус будет побеждён.