В различных отраслях науки и техники могут возникать задачи, в которых требуется рассмотреть большое число возможных вариантов. Иногда это возможно, а иногда — нет или достаточно сложно. Давайте рассмотрим один из подходов к решению таких задач.
Обсудим такую задачу
В левом нижнем углу шахматной доски стоит шахматная фи-гура, которую назовём «полукороль», так как она, в отличие от «настоящего» шахматного короля, ходит только на одно поле строго вправо, или строго вверх, или строго по диагонали вправо вверх. Сколько существует способов переместить фигуру на поле, выделенное серым цветом?
На всех рисунках статьи поля доски чёрного цвета условно не выделены.
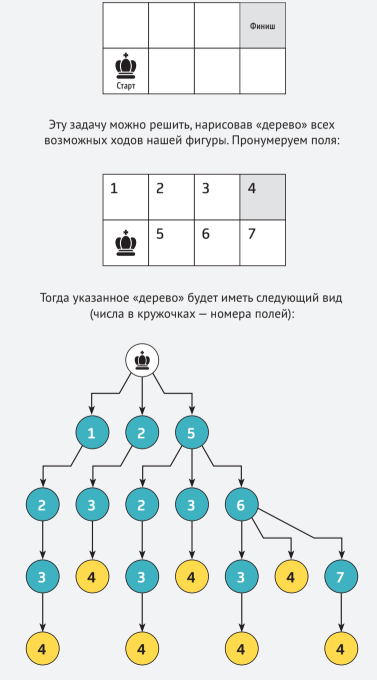
Видно, что искомое общее число маршрутов достижения серого (номер 4) поля равно 7. Однако такой способ решения задачи не очень подходит для случаев, когда полей больше. Имеются более рациональные способы решения задачи, которые можно использовать для любого числа полей. Один из них заключается в анализе маршрутов, так сказать, «с конца». С полей, выделенных ниже чёрным цветом, до цели полукороль может переместиться единственным способом. Запишем это:
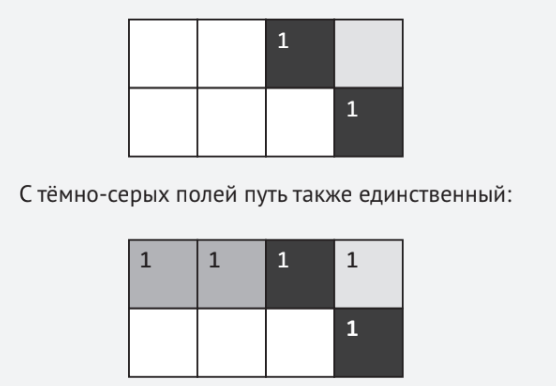
Обсудим теперь число маршрутов со светло-серого поля. С него до «цели» (серого поля) можно попасть непосредственно или через чёрные поля. Так как число маршрутов с чёрных полей нам уже известно (оно записано в этих полях), то общее число путей со светло-серого поля до цели равно 1 (непосредственно) + 1 (через верхнее чёрное поле) + 1 (через правое чёрное поле) = 3. Запишем результат:
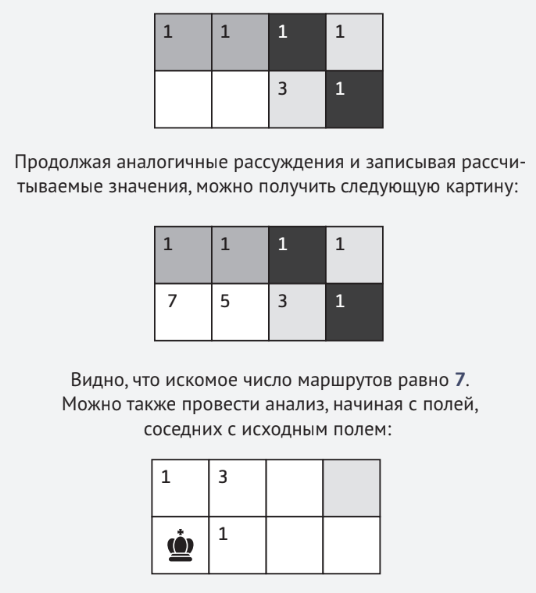
Теперь попробуйте сами
- Нарисуйте граф, моделирующий возможные маршруты фигуры, описанной в статье (граф — конечное число точек на плоскости, соединённых отрезками линий). Используйте номера полей, приведённые на рисунке:
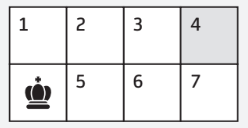
На графе номера полей повторяться не должны.
2. В правом нижнем углу фрагмента шахматной доски стоит шахматная фигура, которую назовём «полукороль», так как она, в отличие от «настоящего» короля, ходит только на одно поле строго влево, или строго вверх, или строго по диагонали влево вверх. Сколько существует способов перемещения фигуры на поле, выделенное серым цветом?

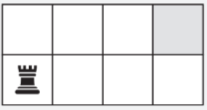
3. В левом нижнем углу шахматной доски стоит шах- матная фигура, которую назовём «полуладья», так как она, в отличие от «настоящей» шахматной ладьи, ходит на любое количество клеток строго вправо или строго вверх. Сколько существует способов перемещения фигуры на поле, выделенное серым цветом?
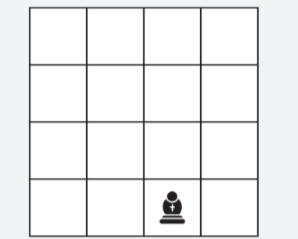
4. В нижнем ряду фрагмента шахматной доски стоит шахматная фигура, которую назовём «полуслон», так как она, в отличие от «настоящего» шахматного слона, ходит на любое количество клеток по диагонали только влево вверх или вправо вверх.
Сколько существует способов перемещения фигуры до верхнего ряда данного фрагмента?
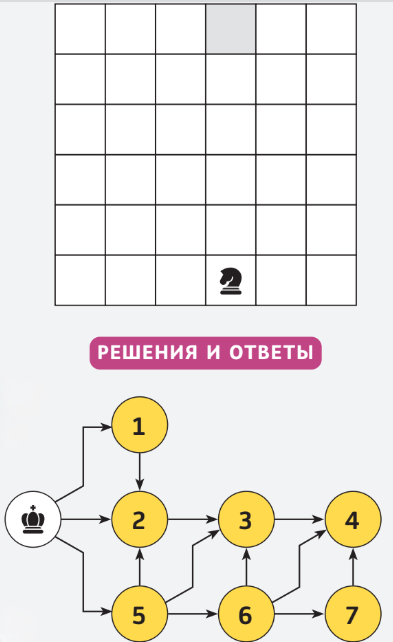
В нижнем ряду фрагмента шахматной доски стоит шахматная фигура, которую назовём «полуконь», так как она ходит как «настоящий» шахматный конь, но только вверх. Сколько существует способов перемещения фигуры на поле, выделенное серым цветом?
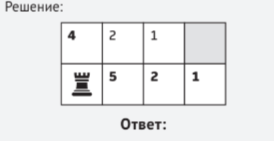
Количество способов перемещения полукороля с той или иной клетки до «цели» приведено в таблице ниже (напомним, что рассмотрение вариантов проводится начиная с конца маршрута).
41 + 9 + 11 = 61
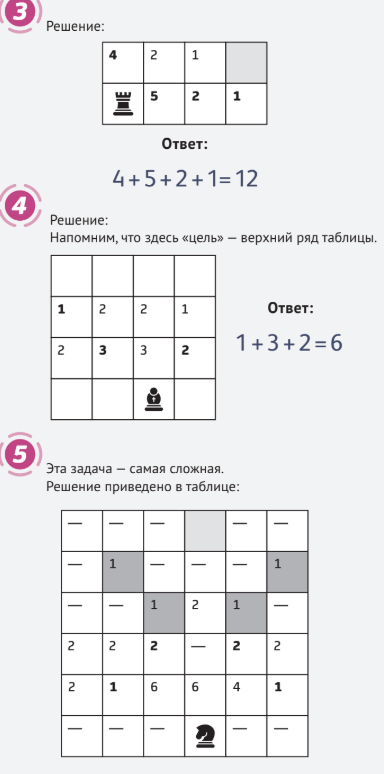
В ней тёмно-серым цветом выделены клетки, с которых до «цели» можно попасть за один ход. В остальных клетках записано количество вариантов маршрутов, которые ведут с них к «цели».
Ответ: 1 + 2 + 2 + 1 = 6
В заключение заметим, что идея анализа возможных вариантов «с конца» лежит в основе так называемого «динамического программирования» — особого метода поиска оптимальных решений в сложных экономических и других задачах. В таких задачах, как правило, количество возможных вариантов решения велико, и рассмотреть их все для выбора лучшего трудно, а иногда и вообще невозможно. Например, если бы в задачах с полукоролём размеры доски были 8 на 8 клеток, то общее число вариантов превысило бы 100 000.
При увеличении размеров это число существенно воз- растает (для условной доски 30 на 30 клеток компьютер, выполняющий 1 000 000 операций в секунду, рассмотрит все возможные варианты перемещения за более чем 100 000 лет!). Поэтому в этих задачах сначала рассматривают небольшое число вариантов «в конце» и выбирают лучшие из них, а затем, «пятясь», выбирают и запоминают лучшие варианты для других состояний. При таком подходе для исходной ситуации уже будут известны все лучшие «будущие» решения, из которых легко можно выбрать наилучший.






