Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа, и вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
Умножение решеткой
Один из них — так называемый «метод решётки». Этим методом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Впервые метод был описан в книге итальянского математика ЛУКИ ПАЧОЛИ «Всё об арифметике, геометрии, отношениях и пропорциях». Она была издана в 1494 году, и в ней — в новой для того времени десятичной системе счисления с использованием арабских цифр — излагались правила и приёмы арифметических действий над целыми и дробными числами, пропорции, задачи на сложные проценты, решение линейных, квадратных и других уравнений. Пачоли приводит пример расчёта произведения методом решётки чисел 987 и 987, причём описывает два варианта этого метода.
В обоих вариантах рисуется таблица с квадратными клетками, в которой количество столбцов равно количеству цифр в множимом, а количество строк — числу цифр в мно- жителе. Клетки разделяются пополам по диагонали. Начнём с варианта, который в книге Пачоли приведён первым (рис. 1).
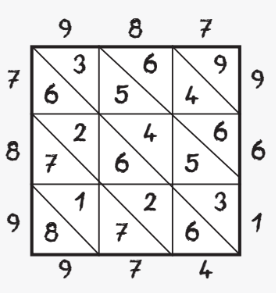
Над таблицей записано число 987 цифрами
слева направо, а с левой стороны вертикально —
цифрами снизу вверх. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая единицы над диагональю, а десятки — под ней.
Результат получается сложением цифр в наклонных полосах. Если при сложении получается двузначная сумма, то укажем только единицы, а десятки прибавим к сумме цифр на следующей полосе. Начинаем с правой верхней клетки: там только одна цифра 9 — её и запишем. Далее в наклонной полосе 6 + 4 + 6, получается 16.
Записываем 6, единица переходит в следующую сумму. Затем 3 + 5 + 4 + 5 + 3 + 1 (единица «осталась» от предыдущей суммы, не забываем) = 21 и т. д.
Результат определяется при чтении полученных цифр, начиная с последней (левой нижней). Итак, получается 974 169. Второй вариант оформления таблицы (см. рис. 2) отличается следующим:
● расположением диагоналей квадратов;
● записью множителя справа (цифры — сверху вниз);
●записью единиц произведения под диагональю, а цифр десятков — над ней.
Суммирование также происходит по наклонным полоскам, начиная с нижней правой клетки, а результат читается от верхней цифры слева от таблицы (974 169).
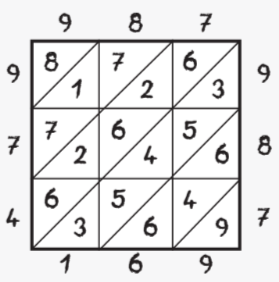
Какой из двух вариантов удобнее — решать вам. Метод решётки именовали также «индийским», «мусульманским» или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского — «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из цифр имели сходство со ставнями-жалюзи, которые закрывали от солнца окна домов. Часто и сегодня описанный метод также называют «метод жалюзи».
Метод решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, притом что количество выполняемых действий в обоих случаях одинаково. Во-первых работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки меньше.
К тому же метод решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Почему это работает?
Возникает вопрос: «Почему метод решётки приводит к правильному ответу?» В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, аналогичной показанной на рис. 2, только перемножаемые числа представим как суммы: 900 + 80 + 7
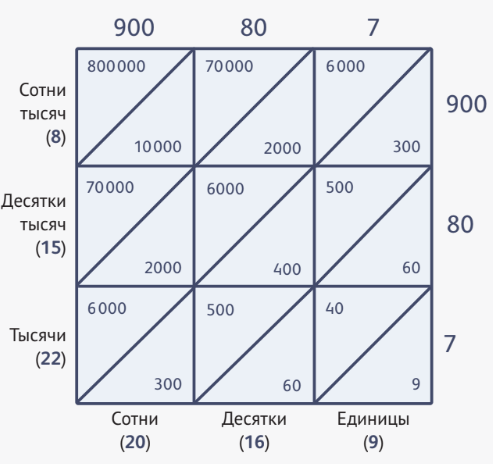
Как видим, в первой наклонной полосе (в правом нижнем углу таблицы) стоят единицы, во второй — десятки, в третьей — сотни и т. д.
При сложении они дают в ответе соответственно число единиц, десятков, сотен и т. д. При дальнейшем сложении получаем искомый результат.
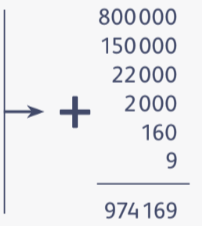
Иначе говоря, в соответствии с законами арифметики произведение чисел 987 и 987 вычисляется так: 987 × 987 = (900 + 80 + 7) × (900 + 80 + 7) = = 810 000 + 72 000 + 6300 + 72 000 + 6400 + 560 + + 6300 + 560 + 49 = 810 000 + (72 000 + 72 000) + +(6300 + 6400 + 6300) + (560 + 560) + 49 = 974 169.
Умножение без бумаги
Серьёзной проблемой метода решётки было то, что для расчётов требовалась бумага — редкая и дорогая в Средневековье. В 1617 году в книге шотландского барона и любителя математики Джона Непера (кстати — изобретателя такого понятия математики, как логарифм) был описан прибор, с помощью которого результат умножения многозначного числа на однозначное определялся без использования бумаги. Устройство состояло из ряда узких пластин, на которых изображены квадратные клетки. В верхней клетке пластины записана одна из цифр от 0 до 9, а остальные разделены диагональю и в них по две цифры. Например, пластина с цифрой 7 выглядела как на рис.

Вы, конечно, уже поняли, что за цифры представлены на ней — в клетках с диагональю записана таблица умножения на число вверху таблицы (7). Все пластины имели вид:
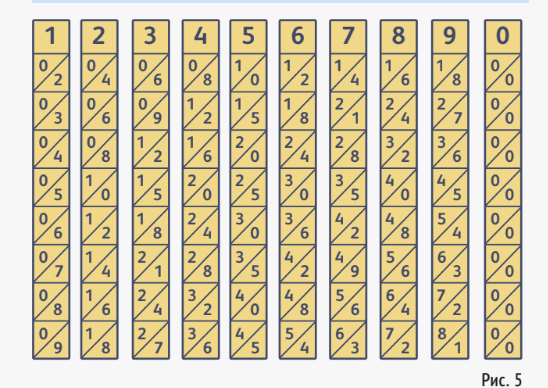
В прибор, который называют «палочки Непера», «пластины Непера», «бруски Непера» и т. п., входила ещё одна пластина с цифрами от 1 до 9. Назовём её «вспомогательной».

Расчёты проводились следующим образом. Пластины
с цифрами числа-множимого размещались так, что их цифры вверху образовывали нужное число.
Пусть, например, это будет число 4938 (см. рис. 7).
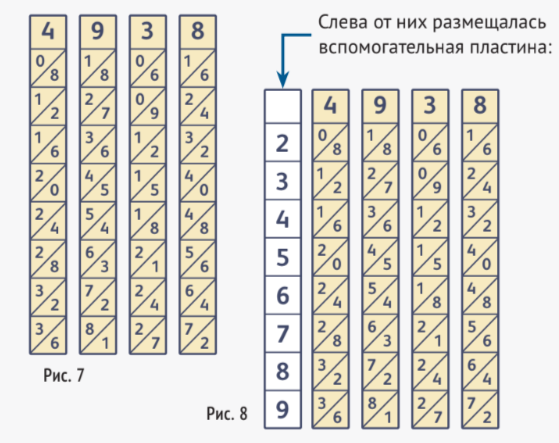
Допустим, что нужно умножить число 4938 на 5. Для этого нужно свободными пластинами выделить строку, соответствующую цифре 5 на вспомогательной пластине (см. рис. 9).
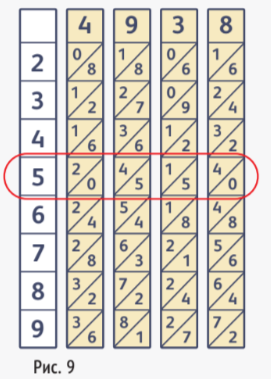
Складываем цифры по наклонным полосам. Начинаем справа налево (как при умножении решёткой — 0, 4 + 5, 1 + 5, 4 + 0, 2), читаем справа налево и получаем результат 24 690.
При помощи пластин. Непера можно перемножать и многозначные числа. Для
этого множимое умножалось на каждую цифру множителя а эти произведения складывались между собой с учётом порядка разрядов.
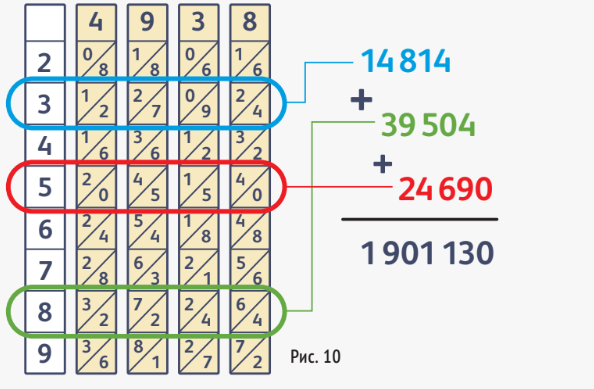
На рис. 10 показан пример умножения числа 4938 на число 385.
Последователи Джона Непера
Прибор Непера не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения числа с повторяющимися цифрами, например 777 227, нужны были несколько комплектов палочек с одинаковыми верх- ними цифрами. Такая проблема решалась заменой пластин узкими брусками, десятигранными призмами или цилиндрами с нанесён- ной на их поверхность таблицей умножения в том же виде, как её представил Непер. Один такой брусок заменял четыре пластины, а призма или цилиндр — даже десять. Ещё одно усовершенствование заключалось в следующем.
При использовании «классических» палочек Непера приходилось складывать числа в уме, часто с учётом переноса из разряда справа, и для каждого разряда запоминать сумму, что, конечно, могло привести к ошибочному результату. В 80-х годах XIX века французский инженер Анри Женай по предложению математика Эдуарда Люка автоматизировал указанные вычисления. Фрагмент прибора, получивший название «Бруски Женая—Люка», показан на рис. 11.
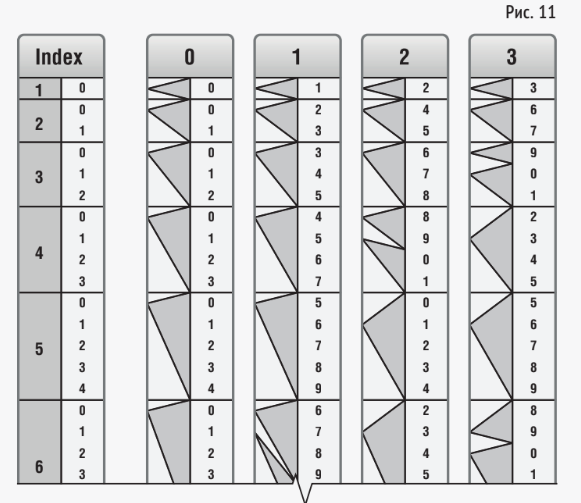
Он состоял из ряда узких деревянных брусков размером 18 × 1,2 × 1 см, на длинных гранях которых были изображены цифры и тёмные треугольники. Как же работали бруски Женая-Люка?

Второй множитель равен 4, поэтому мы смотрим на последний столбец, четвёртую строку. В этой строке верхняя цифра — 6. Это последняя цифра произведения.
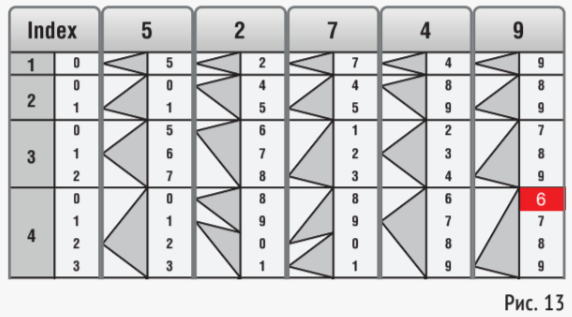
Тёмный треугольник, примыкающий к цифре 6, указывает путь к следующей цифре (9):
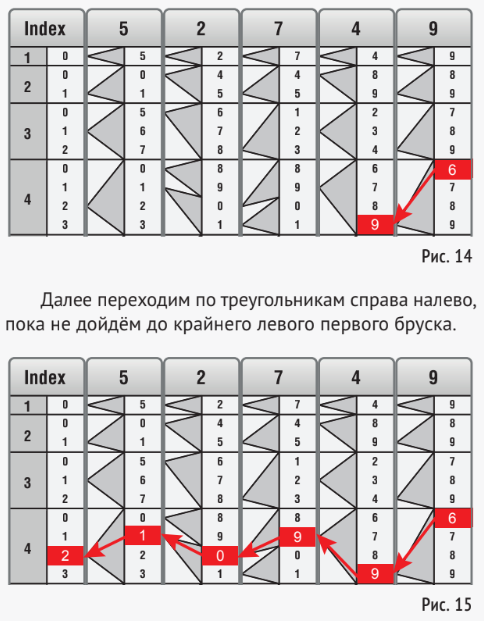
Затем мы просто читаем цифры, которые мы «по- сетили», слева направо. Искомое произведение, показанное красным цветом, равно 210 996. Эффектно, не правда ли? Популярность брусков Женая—Люка была большой, но недолгой: в начале ХХ века их заменили механические счётные приборы — арифмометры. Как говорит- ся, «технический прогресс не остановить». Так закончилась многовековая история старинного метода умножения решёткой…





