Почему многие не любят математику? Один из наиболее частых ответов: из-за её занудства. В любой «очевидной» ситуации заставляют что-то доказывать! Но «очевидные» выводы нередко оказываются ошибочными и долго остаются таковыми, потому что мы интуитивно убеждены в их «правильности».
Для начала проверим наше математическое чутьё — ответим на вопрос: каким будет кратчайший маршрут из точки А в точку В? Думаю, многие сейчас подумали: «Очевидно, отрезок АВ». И вы, конечно, правы. А если я попрошу это доказать? Вот тут-то и возникает тягостное чувство нелюбви к математике. «Зачем? И так всё понятно!» Это интуитивный подход к решению задач: мы полагаем, что знаем ответ, но как он получился, не задумываемся. Зачастую такой подход работает — и даже здорово экономит время. Но давайте-ка попробуем ответить на следующий вопрос.
Сколько существует натуральных чисел от 10 до 20 (включая 10 и 20)? Многие ответят «10», потому что так подсказывает интуиция. И ошибутся, так как правильный ответ — «11». Это можно доказать простым перебором: выписать все числа от 10 до 20 и пересчитать их. Но такое доказательство не совсем универ- сально: а что бы мы делали, если б в задаче фигурировали числа не от 10 до 20, а от 1000 до 2000? Тоже выписывали и считали? Вряд ли. Поэтому будем рассуждать так: от 1 до 20 — 20 натуральных чисел, но нам нужны только те, что от 10, а значит, требуется исключить из рассмотрения все числа от 1 до 9 (именно 9, а не 10!). Останется 20 — 9 = 11, это и есть правильный ответ. Рассуждая аналогично в задаче про 1000 и 2000, получим 2000 — 999 = 1001, а общая формула для чисел от a до b будет: a — b + 1.
Мы привели простые примеры того, как интуиция помогла и ввела в заблуждение. Иначе говоря, интуитивный подход не гарантирует верное решение. В отличие от математики, которая даёт возможность быть уверенным в своей правоте. То есть с доказательствами можно и нужно спорить, они бывают неверными, но по крайней мере у нас есть инструмент, который позволяет обосновать правоту. Конечно, вопрос про числа от 10 до 20 был совсем лёгкий. Давайте рассмотрим ещё несколько контринтуитивных примеров, где угадать верный ответ не так-то просто. Каждую из этих задач попробуйте сперва решить сами, а уж потом читайте дальше. И удивляйтесь.
Задача 1
У арбуза корка в три раза тоньше мякоти (то есть если провести линию от центра арбуза к его поверхности, три четверти этой линии придётся на мякоть, а четверть на корку). Во сколько раз объём мякоти больше объёма корки? Предполагается, что арбуз имеет форму идеального шара, внутри него шар поменьше — мякоть, а дальше корка.

Итак, во сколько же раз объём мякоти больше? В три? В девять? Другие варианты? Интуиция своё дело сделала, теперь за работу берётся математика. Допустим, что арбуз — шар радиусом 4х, внутри которого шар радиусом 3х заполнен мякотью, а всё остальное — корка. Тогда условие выполнено, то есть толщина корки ровно втрое меньше толщины мякоти. По формуле объёма шара V= 4 :3 πR3 получаем, что объём всего арбуза (шара радиусом 4х) равен:
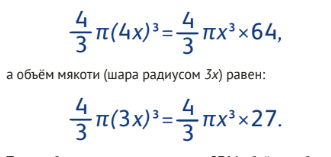
Таким образом, мякоть составляет 2764 объёма арбуза, а корка, соответственно, 3764. То есть объём корки не просто не меньше (в 3, или 9, или сколько вы сказали раз), а почти в полтора раза больше объёма мякоти… Вот так логика и несложные расчёты опровергли интуитивное соображение.
Задача 2
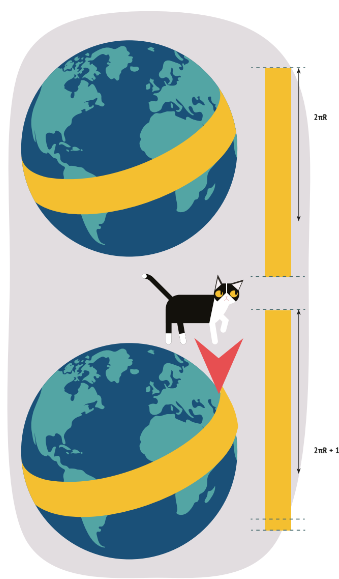
Земной шар опоясали лентой, плотно прилегающей к земле. Затем ленту увеличили на 1 метр и равномерно распре- делили вдоль поверхности планеты. Сможет ли в получившийся зазор пролезть кошка? Опять же оговоримся: мы предполагаем, что Земля имеет форму шара, хотя это и не совсем верно. Итак, каким будет ответ? Интуиция подсказывает, что кошка пролезть не должна, не так ли? Ведь если опоясать Землю по экватору, длина ленты окажется около 40 000 километров, так что увеличение на 1 метр вряд ли будет заметно.
И если дальше мы равномерно отодвинем ленту от земли, в полученный микроскопический зазор не то что кошка — муравей вряд ли пролезет. Так? А вот и нет!
Допустим, радиус земного шара равен R метров (в реальности он составляет чуть больше 6 тысяч километров, но в данной задаче и это не принципиально). Тогда лента имеет длину 2πR метров по формуле длины окружности. Соответственно, когда мы увеличиваем длину на 1 метр, она получается равной (2πR + 1) метров. При этом, если мы равномерно отодвигаем ленту от поверхности, то лен- та и теперь образует окружность, только радиус у неё другой — допустим, R 1 . Заметим, что в этом случае длина ленты равна 2πR 1 . Но она же посчитана у нас парой строк выше! Приравняем:
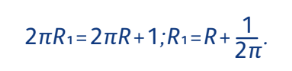
Задача 3
Задача 3 В комнате собрались 50 человек. Какова вероятность, что среди них найдутся двое родившихся в один день? Опять же, сделаем необходимую оговорку: среди них нет близнецов, иначе задача была бы неинтересной. Ну и каков ваш интуитивный ответ? Процентов 10–20, на- верное? Действительно, в году 365 дней, у нас 50 человек, а это меньше, чем седьмая часть. Значит, что-то около 100:7, то есть примерно 15%. Так? Или, может, у кого-то 30? А теперь подключим математику. Посчитаем вероятность того, что все собравшиеся родились в разные дни (так будет проще), а затем вычтем полученный результат из единицы. Это и будет искомый ответ — вероятность, что в комнате найдётся пара чело- век, появившихся на свет в один день (может, и не одна пара, но об этом нас не спрашивали; главное, чтобы были хоть двое).
Возьмём первого человека — он родился в какой-то определённый день. Рассмотрим второго — у него есть 365 вариантов, из которых нам подходят 364 (чтобы не совпало с первым). Значит, вероятность, что первый и второй родились в разные дни, равна 364 365. Теперь возьмём третьего. У него 363 варианта из 365, то есть он родился не в тот же день, что первый или второй, с вероятностью 363 365. Но тогда по правилу произведения вероятность того, что все трое родились в разные дни, равна 364 365 × 363 365 . Аналогично дело обстоит с четвёртым, пятым и так далее до пятидесятого. Значит, вероятность, что все они родились в разные дни, равна:
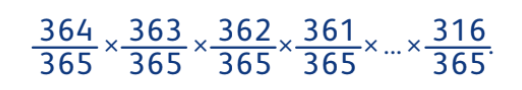
Почему 316? А потому, что дробь, соответствующая второму человеку, имеет числитель 364 (365 — 1), третьему — 363 (365 — 2). Таким образом, для 50-го человека числитель будет 316 (365 — 49). Конечно, посчитать это без калькулятора сложно, но даже очень грубая прикидка кое-что даёт. Например, если перемно- жить только две последние дроби 316 365 × 317 365 , результат уже будет меньше 0,76, то есть искомая вероятность (напомним, для её полу- чения результат умножения нужно вычесть из единицы) больше 24%.

Если же перемножить все дроби, вероятность будет… 97%! Поверить в это сложно, но это так. А знаете, когда вероятность составит около 50%? Уже в случае 23 человек! Кстати, это можно легко проверить. Возьмите несколько классов — там как раз человек по 25–30. И посмотрите, как часто повторяются дни рождения у одноклассников. Вы удивитесь результату!
Мы тоже решили проверить эти выкладки и посмотрели составы футбольных сборных на Кубке конфедераций. Там было 8 сборных по 23 человека — вы не поверите, но в четырёх командах были игроки, родившиеся в один день! Практика прекрасно подтвердила теорию. Что ж, рассмотрев несколько примеров, мы убедились, что чутьё периодически нас подводит. Так что относитесь к интуитивным выводам аккуратно, подвергая их сомнению и стараясь доказывать. Надеемся, отныне интуиция с логикой будут каждый день помогать вам двигаться вперёд, к достижению целей, ведь, как показывает ещё один контринтуитивный факт, 1,01365 ≈ 37,8,а 0,99365 ≈ 0,03!
Фото: Unsplash






