Слышали вы такое словосочетание — «прокрустово ложе»? Речь о мифическом греческом разбойнике Прокрусте, который, кстати, вовсе не был простым парнем с большой дороги, а доводился сыном самому повелителю морей Посейдону! Так вот, этот самый Прокруст хитростью заманивал путников в свой дом, где укладывал их на ложе и «уравнивал» под его размеры: кому кровать была велика — вытягивал, кому коротка — отрубал ноги. Что он делал с теми, кому кровать оказывалась впору, история умалчивает. В любом случае древние греки высоко ценили справедливость, так что закончил жизнь Прокруст на своём же ложе. Но его идея нашла неожиданное применение в математике.
Выражение «прокрустово ложе» давно стало крылатым и означает жёсткое уравнивание, ради которого жертвуют чем-то существенным. Несмотря на негативный смысл этого фразеологизма, идея уравнивать различающиеся объекты находит применение в математических задачах. Но не бойтесь: никому ничего отрубать мы не будем — просто воспользуемся сходным принципом.
ЗАДАЧА 1. НА ДВУХ ПОЛКАХ В СУММЕ СТОИТ 30 КНИГ, ПРИ ЭТОМ НА ОДНОЙ ПОЛКЕ ИХ НА 4 БОЛЬШЕ, ЧЕМ НА ДРУГОЙ. СКОЛЬКО КНИГ НА КАЖДОЙ ПОЛКЕ?
Конечно, эту задачу можно решить подбором — правда, тут сразу встаёт вопрос о единственности найденного решения. Можно ввести переменную, обозначив через x количество книг на одной из полок, а затем решить уравнение. Но, во-первых, это долго оформлять, а во-вторых, составлять и решать уравнения мы учимся далеко не сразу, а метод Прокруста не требует ничего, кроме умения считать. Итак, попробуем уравнять книги на полках. Нам известно, что на одной полке на 4 книги больше, вот и уберём их, причём не переставим на другую полку, а просто отложим.

Получается, что теперь книг на полках поровну! Правда, в сумме их уже не 30 (мы же убрали 4 книги), а 26. Стало быть, на каждой полке по 13 книг (26 : 2, ведь книг стало поровну). Осталось вернуть 4 книги на место и получить окончательный ответ: на одной полке 13 книг, на другой — 17. Что же помогло нам решить задачу? Мы использовали идею Прокруста в мирных целях — уравняли количество книг на полках, после чего разделили получившееся число пополам и ответили на поставленный вопрос. Рассмотрим ещё один пример.
ЗАДАЧА 2. В ШКОЛЕ ТРИ МАТЕМАТИЧЕСКИХ КРУЖКА: ДЛЯ ПЕРВОГО КЛАССА, ДЛЯ ВТОРОГО И ТРЕТЬЕГО. В ПЕРВОМ КРУЖКЕ ЗАНИМАЕТСЯ НА ДВА ЧЕЛОВЕКА БОЛЬШЕ, ЧЕМ ВО ВТОРОМ, А ВО ВТОРОМ — НА ТРИ ЧЕЛОВЕКА БОЛЬШЕ, ЧЕМ В ТРЕТЬЕМ. ВСЕГО В КРУЖКАХ ЗАНИМАЕТСЯ 65 УЧЕНИКОВ. СКОЛЬКО ЧЕЛОВЕК ХОДИТ В КАЖДЫЙ КРУЖОК?
Итак, в первом кружке занимается на два человека больше, чем во втором. Давайте уравняем количество кружковцев. Нет-нет, никакого самоуправства по отношению к двум первоклассникам мы не допустим! Предположим, что они просто пропускают занятие по уважительной причине. Тогда в первых двух кружках детей будет поровну, при этом общее их количество уменьшится на два и составит 63. В третий кружок ходит на три человека меньше, чем во второй (напомним, количество учащихся во втором кружке мы не меняли).

Уравниваем: допустим, что в третий кружок записались ещё три человека. Тогда во всех трёх кружках учеников станет поровну, а их общее количество будет равно 66. Стало быть, в каждом кружке занимается по 22 человека! Осталось получить окончательный ответ. Второй кружок мы не трогали, так что в нём и исходно было 22 человека. В первом до выравнивания было на два ученика больше, то есть там занимались 24 первоклассника. Наконец, в третий мы добавили трёх человек, а значит, на самом деле кружок посещали 19 третьеклассников. Победа! Аналогично решаются задачи и в случае, когда объектов не три, а больше. Но мы лучше разберём другой случай. Речь пойдёт о так называемой задаче про головы и ноги. Как ни странно, Прокруст здесь почти ни при чём. Как и в прошлой задаче, ни одна нога или голова не пострадает. Хотя… Впрочем, перейдём к делу.
ЗАДАЧА 3. ПО ДВОРУ ХОДЯТ КУРЫ И КОЗЫ. ВАСЯ НАСЧИТАЛ ВО ДВОРЕ 20 ГОЛОВ И 48 НОГ (СВОИ ГОЛОВУ И НОГИ ОН НЕ СЧИТАЛ). СКОЛЬКО КУР И СКОЛЬКО КОЗ ХОДИТ ПО ДВОРУ?
В чём здесь проблема? В том, что ног у коз и кур не поровну. Действительно, если бы речь шла только о курах, мы бы раздели- ли количество ног пополам — и готово (правда, тогда количество голов было бы лишней информацией). Аналогично с козами, только делить пришлось бы на четыре. А так у кого-то во дворе по две ноги, а у кого-то по четыре. Что же делать?

А давайте уравняем! Пусть у коз тоже будет по две ноги, а не по четыре. Но так как мы обещали никому ничего не ру- бить, давайте просто мысленно поставим коз на задние ноги, а передние пусть болтаются в воздухе. Тогда, раз животных по двору гуляет 20 (столько же, сколько голов), на земле находится 40 ног — по две на каждое животное. При этом Вася насчитал 48 ног, то есть ещё 8 конечностей остались неучтёнными. Позвольте, но ведь козы встали на задние ноги, а передние мы не считали! Значит, их-то как раз и восемь. Поскольку у каждой козы по две передних ноги, то всего коз 8 : 2 = 4. Итого: по двору ходят 4 козы и 16 кур.
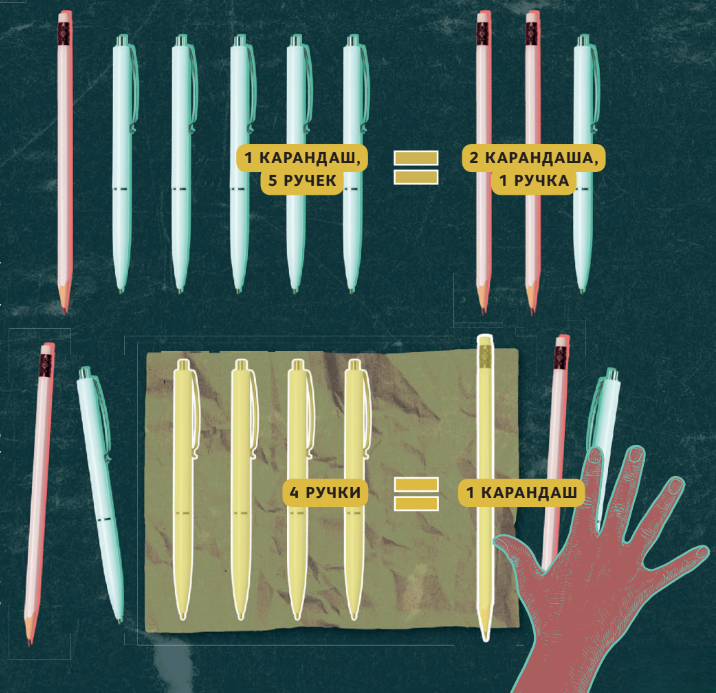
ЗАДАЧА 4. ПЯТЬ РУЧЕК И ОДИН КАРАНДАШ СТОЯТ СТОЛЬКО ЖЕ, СКОЛЬКО ОДНА РУЧКА И ДВА КАРАНДАША. ВО СКОЛЬКО РАЗ КАРАНДАШ ДОРОЖЕ РУЧКИ?
Сразу оговоримся: предполагается, что все ручки стоят одинаково, все карандаши — тоже. Эту задачу, конечно, можно решить, введя две переменные. Но зачем стрелять из пушки по воробьям, когда есть короткое и элегантное решение? Допустим, в одной кучке лежат пять ручек и карандаш, в другой — два карандаша и ручка. Уберём из них общее: один карандаш и одну ручку. Оставшиеся наборы канцтоваров будут стоить по-прежнему одинаково, не так ли? При этом в первой кучке останется четыре ручки, а во второй — один карандаш (да-да, так себе «кучка» из одного предмета… Впрочем, про парадокс кучи и нечёткую логику мы ещё поговорим в одном из будущих номеров). Значит, карандаш стоит в четыре раза больше, чем ручка.
Что помогло решить задачу? Умение отрезать лишнее, оставив объекты равными. Эта же идея, навеянная деяниями Прокруста, применима и в чуть более сложных ситуациях.
ЗАДАЧА 5. ГРАВИРОВЩИК ДЕЛАЕТ ТАБЛИЧКИ С БУКВАМИ. ОДИНАКОВЫЕ БУКВЫ ОН ГРАВИРУЕТ ЗА ОДНО И ТО ЖЕ ВРЕМЯ, РАЗНЫЕ — ВОЗМОЖНО, ЗА РАЗНОЕ. НА ТАБЛИЧКИ «ДОМ МОДЫ» И «ВХОД» ОН ПОТРАТИЛ 50 МИНУТ, А ТАБЛИЧКУ «В ДЫМОХОД» СДЕЛАЛ ЗА 35 МИНУТ. ЗА КАКОЕ ВРЕМЯ ОН СДЕЛАЕТ ТАБЛИЧКУ «ВЫХОД»?

ЗАДАЧА 6. ТОРТ УПАКОВАН В КОРОБКУ С КВАДРАТНЫМ ОСНОВАНИЕМ. ВЫСОТА КОРОБКИ ВДВОЕ МЕНЬШЕ СТОРОНЫ ЭТОГО КВАДРАТА. С ПОМОЩЬЮ ЛЕНТОЧКИ ДЛИНОЙ 156 СМ КОРОБКУ МОЖНО ПЕРЕВЯЗАТЬ И СДЕЛАТЬ СВЕРХУ БАНТИК (КАК НА РИСУНКЕ СЛЕВА). А ЧТОБЫ ПЕРЕВЯЗАТЬ ЕЁ С ТОЧНО ТАКИМ ЖЕ БАНТИКОМ СБОКУ (КАК НА РИСУНКЕ СПРАВА), НУЖНА ЛЕНТОЧКА ДЛИНОЙ 178 СМ. НАЙДИТЕ РАЗМЕРЫ КОРОБКИ.
Попробуем опять-таки не думать про уравнения, а поищем общее у указанных способов. Понятно, что в первом случае есть четыре части ленты, опоясывающие коробку по бокам (короткие), четыре — сверху и снизу (длинные), а также бантик. Во втором случае есть две короткие части ленты (по одной слева и справа), шесть длинных и такой же бантик.
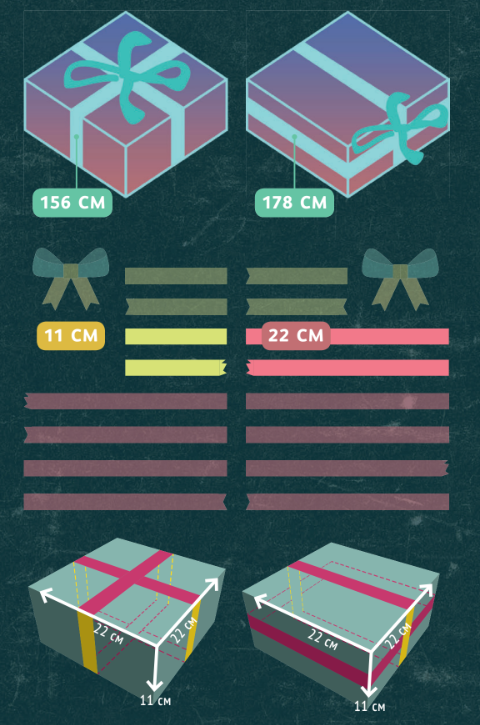
При этом второй способ «длиннее» первого на 22 см. И если мы уберём общее, разница останется такой же. Что же общего у этих споcобов? Две короткие части, четыре длинные и бантик. Убрав их, получаем, что оставшиеся в первом случае две короткие части ленты короче двух длинных (во втором случае) на 22 см. А значит, короткая часть меньше длинной на 11 см. Осталось вспомнить, что короткая часть составляет половину длинной, то есть короче её на свою же длину.
Таким образом, длина короткой части — 11 см, а длинной — 22 см. Окончательные размеры коробки: 11 х 22 х 22. Что ж, выходит, даже жестокие разбойники с их варварскими методами могут сослужить потомкам неплохую службу. Нужно лишь отделить идею от злодеяний и найти ей мирную сферу применения.






