Счастье за деньги не купишь, гласит народная мудрость. Зато можно, хоть и случайно, купить счастливый билетик. Мы воспринимаем это событие как удачу, потому что оцениваем его вероятность как низкую. Но так ли уж редко это происходит на самом деле?
Сперва проясним, что такое счастливый билет. Любой билет, в кино или на поезд, имеет уникальный номер. Как правило, его присваивают последовательно: начиная с 0 и до некоторого значения. Делается это для удобства учёта. Мы будем рассматривать билеты, у которых номер состоит из 6 цифр: от 000000 до 999999. Определений счастливого билета несколько, но мы остановимся на наиболее популярном: билет называется счастливым, если сумма первых трёх цифр его номера равна сумме последних трёх цифр. Прежде чем начать охоту за билетами, давайте ответим на частые вопросы, с ними связанные. В этом нам поможет математика.
Могут ли два счастливых билета идти подряд?
Переведём этот вопрос на формальный язык математики: существует ли такой счастливый билет ABCDEF, что ABCDEF + 1 тоже будет счастливым? Иначе говоря, для этих чисел должно выполняться равенство:
A + B + C = D + E + F
A + B + C = D + E + F + 1
Если первое из шестизначных чисел оканчивается не на 9 (F9), то при прибавлении единицы сумма последних трёх цифр изменится, а первых трёх нет, значит, билет перестанет быть счастливым. Если же на конце было 9 (F = 9), то сумма последних трёх цифр уменьшится (если на конце более трёх девяток, то уменьшится и сумма первых трёх, но не настолько). Итак, счастливые билеты подряд не идут. Но, с другой стороны, подряд они могут идти через девятку: например, 100001 и 100010. Более того, иногда цепочка «через девять» бывает весьма длинной: 900009, 900018, 900027, …, 900090. Это если нам повезло с началом. А если начало — 998999? Тогда ближайший счастливый билет будет аж через тысячу! Действительно, дальше все билеты будут начинаться с 999, так что на конце для счастья тоже надо иметь 999…
Предварительная оценка
Для начала попробуем приблизительно оценить их количество. Несложная оценка снизу: нам подходят все билеты вида АВСАВС. Сколько таких билетов? А столько же, сколько всего комбинаций первых трёх цифр — 1 000. Так что счастливых билетов точно не меньше 1 000. Неплохо, но мы не учли кучу вариантов, когда цифры разные — например, те же 900018. Можно попытаться учесть перестановки цифр АВС, то есть билеты вида АВСВСА, АВСАСВ и т. д. Но, увы, просто умножить на 6 (количество возможных перестановок цифр А, В и С) не получится: если среди них есть совпадающие цифры, то мы имеем уже не 6 вариантов, а 3 или 1.
Впрочем, эту идею можно реализовать по-другому. Рассмотрим все комбинации следующего вида: на первых трёх местах стоят цифры А, В и С, на вторых трёх — те же цифры, но в произвольном порядке. Сколько же таких вариантов набежит? На первом месте может стоять любая из 10 цифр, то есть пока 10 вариантов. Для любой первой цифры есть 9 вариантов второй, значит, их уже 90. Для каждого из этих 90 существует 8 вариантов третьей цифры — всего, стало быть, 720. И теперь нам осталось умножить 720 на количество способов переставить три фиксированные различные цифры по оставшимся трём местам.
Как мы уже поняли, таких вариантов 6, значит, общее количество чисел — 4 320. Однако и это оценка снизу, причём «сильно снизу»: мы всё ещё не учитываем варианты с разными цифрами. Хорошо, попробуем теперь оценить искомую сумму сверху. Заметим, что, если каждый счастливый билет ABCDEF заменить на билет ADBECF, количество не изменится, значит, можно просто посчитать количество шестизначных чисел, у которых сумма цифр на чётных местах равна сумме на нечётных. А это очень похоже на признак делимости на 11! Напомним, если в числе разность между суммой цифр на чётных и нечётных местах делится на 11, то и число делится на 11. Значит, все наши счастливые билеты «второго типа» делятся на 11, а тогда их не больше, чем чисел, делящихся на 11, то есть 90909 (1000000 : 11). Получается, что счастливых билетов не больше 90909. Впрочем, это также очень грубая оценка, ведь вовсе не каждое число, делящееся на 11, имеет равные суммы цифр на чётных и нечётных местах — например, 000506. Так что счастливых билетов существенно меньше. Давайте же точно подсчитаем, сколько их!
Расчет и результат
Чтобы посчитать точное количество, заменим каждую из трёх последних цифр на дополняющую её до 9. D заменим на K = (9 – D), E на M = (9 – E), F на N = (9 – F). Так как исходно A + B + C = D + E + F, то теперь для числа ABCKMN:
A + B + C + K + M + N
=
A + B + C + 9 – D + 9 –E + 9 – F
=
27
Итак, количество счастливых билетов в точности равно количеству чисел от 000000 до 999999, сумма цифр которых равна 27. Стало немного легче, но предстоит ещё немало работы. Сперва вычислим искомое количество. Для этого нарисуем таблицу, в которой по горизонтали укажем количество используемых цифр, а по вертикали — искомую сумму. Таким образом мы последовательно ответим на все вопросы вида «Сколько существует способов представить число k в виде суммы n цифр». Делать это мы будем рекурсивно, то есть выражать большие значения через меньшие. Поехали! Очевидно, что в первом столбце у нас будет по одному способу получить числа от 0 до 9 (с помощью одной цифры), а всё, что больше 9, — 0 способов.

Далее, если перейти ко второму столбцу и взять, допустим, число на пересечении второго столбца и шестой строки (k = 5), сколько существует способов представить 5 в виде суммы двух цифр? Логика тут простая. В качестве второй цифры мы можем выбрать любой из вариантов от 0 до 5. Если выбираем 0, то сумма всех цифр, кроме второй, должна быть равна 5 (да-да, понятно, что в данном случае «всех, кроме второй» — это только первая цифра, но давайте сразу составим алгоритм в общем виде). Если выбираем в качестве второй цифры 1, то сумма оставшихся должна быть равна 4 и т. д. Но ведь тогда мы просто должны сложить способы из предыдущего столбца — для всех чисел от 0 до 5! И получить 6 вариантов. Ещё пример: допустим, я хочу заполнить во втором столбце поле для k = 11. Несложно увидеть, что тогда вторая цифра 0 или 1 не даёт ни одного варианта, так как первая не может быть больше 9. Иначе говоря, мы обращаемся к пустым ячейкам первого столбца, которые соответствуют k = 10 и k = 11. Впрочем, можно считать, что там не пустота, а нули — это не важно.
А можно ли как-то попроще, не складывая тонну чисел?
Да, есть и более короткая комбинаторная формула, но вывести её гораздо сложнее. Не будем приводить полное рассуждение — лишь обозначим идею и выпишем окончательную формулу. Идея в следующем: вернёмся к тому, что нам надо посчитать количество способов представить 27 как сумму 6 цифр. Сделаем это так: возьмём 27 яблок и поставим среди них 5 перегородок. Тогда количество яблок до первой перегородки будет первым слагаемым суммы, от первой перегородки до второй — вторым слагаемым и т. д. Обратите внимание, что перегородки могут стоять подряд, и в этом случае слагаемое окажется равным нулю. Значит, задача сводится к подсчёту количества способов расставить перегородки. Но заметим, что всего у нас получилось 32 объекта (27 яблок и 5 перегородок) и мы должны выбрать местоположение для 5 перегородок (на остальные места встанут яблоки). Сколько же существует способов выбрать 5 мест из 32? C32, если вы знакомы с комбинаторикой (впрочем, если не знакомы — столько же). Проблема в том, что это ещё не ответ. Мы посчитали количество способов представить 27 в виде суммы 6 слагаемых, но пока не учли, что ни одно слагаемое не должно быть больше 9. Если же учесть это, итоговая формула будет такой:
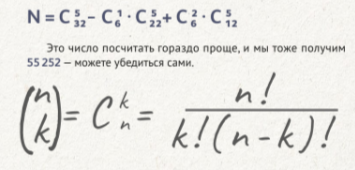
Итак, что же мы получили? Мы вычислили, что примерно 5,5% билетов являются счастливыми, — иначе говоря, в среднем каждый восемнадцатый. Не так уж и редко, оказывается! А вот оправдается ли статистика на практике, проверяйте сами. И помните, что если съесть такой билетик раньше времени, то кроме отравления можно заработать ещё и немаленький штраф от контролёра, что мало соответствует представлениям большинства о счастье. Зато счастье от решения непростой задачи у нас никто не отнимет. До новых счастливых встреч!






