Царица наук, гимнастика для ума, источник вдохновения — как только математику ни называют. Но всё это не просто высокопарные слова. Поверьте нам. Если математика кажется скучной или, наоборот, вы считаете, что знаете этот предмет на пять, то вот вам десяток необычных математических объектов, которые заставят взглянуть на неё по-новому. Внимание! Приготовьте фантазию и ум, мы начинаем.
1. Труба Торричелли
Ученик Галиев, итальянский математик и физик Эванджелиста Торричелли известен прежде всего идеями об атмосферном давлении и новой механике. Торричелли также обнаружил интересный математический объект с необычным свойством. Давайте сперва его построим: для этого нарисуем функцию f(x) = 1/x и рассмотрим её график на отрезке от 1 до бесконечности. Если вращать этот график относительно оси x, мы получим объект, напоминающий рог.
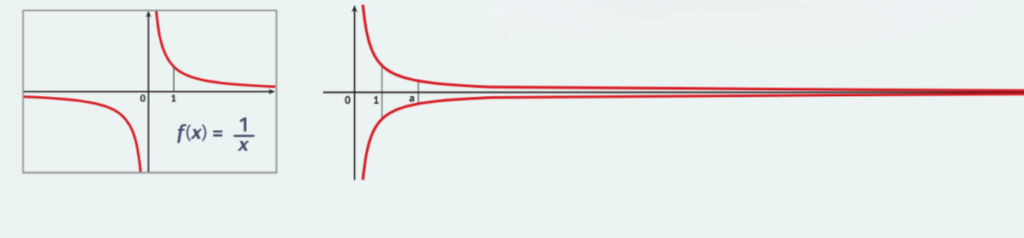
Что же в нём такого необычного? Труба Торричелли, именно такое название получил объект, имеет бесконечную площадь поверхности, но конечный объём. Иначе говоря, вы сможете наполнить его жидкостью, но вам не хватит никакой краски, чтобы его покрасить. Убедиться в этом можно, посчитав объём и площадь поверхности трубы. Для этого нам понадобится высшая алгебра, поэтому часть формульных выводов опустим. Этой формулой вычисляется объём нашего рога на отрезке от 1 до a:

При устремлении а к бесконечности площадь также будет стремиться к бесконечности. Часто трубу Торричелли называют рогом Гавриила — именно его звук пробудит мёртвых в Судный день, согласно христианскому вероучению. Интересно объяснение этого названия: рог тоже связывает бесконечное с конечным.
2. Магический квадрат Ло-Шу
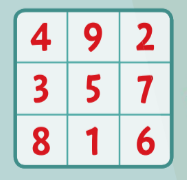
Согласно древней китайской легенде, во времена правления великого императора Юй в Поднебесной произошло небывалое наводнение. Все силы страны были брошены на борьбу с его по- следствиями. Даже сам император принял участие в работах, и в один из дней перед ним из воды показалась огромная черепаха с любопытным рисунком на панцире. Юй увидел, что поверхность разделена на 9 секторов, заполненных точками — в каждом секторе от 1 до 9. Как бы император ни складывал эти точки, по горизонтали, вертикали или диагонали, всегда получалось число 15.
Математики называют такие квадраты нормальными магическими квадратами. Суммы чисел в столбцах, строках и диагоналях в таком квадрате равны. Более того, если сторона квадрата равна n, он должен быть заполнен числами от 1 до n2. В Китае Ло-Шу (в переводе — речной свиток) буквально стал одним из символов фэн-шуй — искусства правильно располагать объекты относительно потока «природной энергии» ци, а также он участвует в множестве гадательных практик. Для математиков же Ло-Шу уникален: это единственный нормальный магический квадрат размера 3×3 (остальные получены путем его вращения).
Сегодня математики разработали множество методов построения магических квадратов любой размерности. Имеют ли они практическую ценность? Безусловно. Магические квадраты могут быть использованы в производстве матриц дисплеев экранов — благодаря им можно добиться плавности перехода цвета или яркости в изображении.
3. Треугольник Рёло
Немецкий инженер Франц Рёло — один из отцов теории машин и механизмов. Его именем названа простейшая после круга фигура, которая имеет постоянную ширину. Что это? Легче всего это объяснить на примере. Если к треугольнику Рёло провести пару параллельных прямых, то они останутся параллельными вне зависимости от направления треугольника. вне зависимости от направления треугольника.

Попытаемся понять, почему треугольник Рёло имеет постоянную ширину. Для этого построим его. Сперва нарисуем обычный равносторонний треугольник, далее циркулем отложим три окружности с одинаковым радиусом с центрами на вершинах этого треугольника. Из построения видно, что расстояние от вершины нового треугольника до любой точки противоположной стороны равно радиусу окружности, а радиусы у окружностей одинаковы.
Среди других фигур с одинаковой постоянной шириной треугольник Рёло имеет наименьшую площадь и симметричен относительно центра. Но самое удивительное то, что и у этого математического объекта есть практическое применение: сверлом формы треугольника Рёло можно просверлить квадратное отверстие с немного скруглёнными уголками. Разница в площади от квадрата с аналогичными сторонами будет около 2 %. Но такое сверло должно вращаться, не просто вокруг своей оси, а по особой траектории — центр сверла должен двигаться по кривой сильно похожей на окружность (на самом деле это пересечение четырёх дуг эллипсов).
4. Бутылка Клейна
Немецкий математик Феликс Клейн придумал объект, который имел бы только одну сторону и при этом не имел бы краёв. Что значит «одна сторона»? Представьте себе, что вы начали прогулку по поверхности такого объекта, а ваша обувь оставляла бы красные следы. Исходив его вдоль и поперёк, вы обнаружили бы, что вся поверхность объекта красная, но вы ни разу не перешагивали через его край. Звучит удивительно, но это возможно. Чтобы осознать это, вам следует знать, что при рассечении бутылки Клейна получается другой интересный объект с одной поверхностью — лента Мёбиуса.
Попробуйте провести прямую вдоль ленты не отрывая руки. Через некоторое время вы вернётесь к начальной точке. Бутылка Клейна на самом деле четырёхмерный объект, поэтому использовать его в нашем трёхмерном пространстве в полной мере невозможно. В нашем измерении у бутылки появляется участок самопересечения, которого не будет в четырёхмерном. Также Клейн знаменит тем, что первым строго доказал непротиворечивость геометрии Лобачевского.

5. Кривая Пеано
Она же кривая, заполняющая пространство. Была предложена итальянским математиком Джузеппе Пеано. Эта кривая проходит через все точки квадрата и куба, в двумерном или трёхмерном пространстве соответственно. Особенность кривой Пеано в том, что это непрерывная функция, которая связывает все точки отрезка со всеми точками квадрата на плоскости. Тем самым Пеано показал, как множество меньшей размерности может быть связано с множеством большей размерности.
6. Снежинка Коха
Шведский математик Нильс Фабиан Хельге фон Кох предложил идею самоподобной кривой, сегодня известной как снежинка Коха. Самоподобным, или фрактальным называют объект, в точности или приближённо совпадающий со своей частью. Опять же, чтобы понять, построим эту снежинку. Для этого нарисуем равносторонний треугольник, каждую сторону поделим на три части и отложим на них новые равносторонние треугольники, и будем продолжать бесконечно долго — с каждым из образованных треугольников. В результате, мы получим фигуру, напоминающую снежинку. Она примечательна тем, что её периметр имеет бесконечную длину, а площадь ограничена. Давайте проверим это.
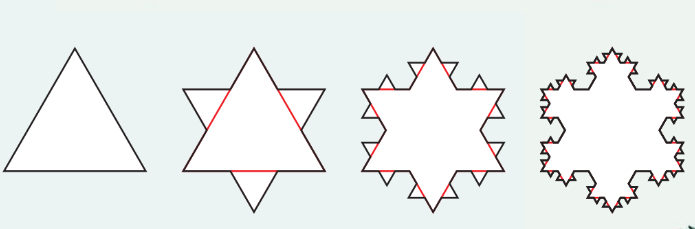
Каждая итерация умножает количество сторон снежинки Коха на четыре, поэтому число сторон после n повторений будет равно:

7. Ковёр Серпинского и губка Менгера
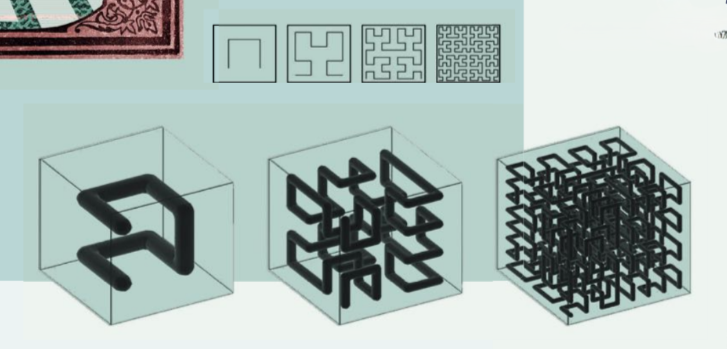
Ковёр Серпинского — это двумерный объект, предложенный польским математиком Вацловом Серписким. А губка Менгера — его трёхмерный вариант. Ковёр получается из начального квадрата последовательным вырезанием серединных квадратов, длина которых равна 1⁄3 от большего квадрата. Далее эту процедуру проделываем с каждым квадратом. В результате получим квадрат с бесконечным количеством дырок, аналогично строится и губка Менгера. Как видно из построения, и ковёр и губка самоподобны, то есть имеют фрактальные свойства.

Удивительным свойством губки Менгера является то, что по мере увеличения площади поверхности уменьшается её объем — и, значит, при бесконечной площади объём губки будет равен нулю. Аналогично с ковром Серпинского: при бесконечном периметре нулю будет равна его площадь.






