Как любят шутить программисты, есть 10 типов людей: те, кто понимает двоичную систему счисления, и те, кто её не понимает. А вот используют её все без исключения, порой сами этого не подозревая. Например, при обмене сообщениями. На каком бы языке вы ни писали, компьютер переведёт ваши слова в 0 и 1. Далее он отправит этот цифровой набор по каналам связи вашему собеседнику. Звучит легко и просто? Но на практике вы столкнётесь с сотнями сложнейших проблем. Мы расскажем об одном их решении, предложенном выдающимся математиком Ричардом Хэммингом.
ДЕЛО В ОБЪЁМЕ
Каждый современный человек имеет общее представление о том, как работает компьютер. И для него не секрет, что информация хранится, обрабатывается и передаётся в двоичной системе счисления. Представим себе, что язык, на котором мы говорим, состоял бы только из двух букв — А и B. Слова выглядели бы как последовательности — например, АBBA или BBA. Как бы мы передавали сообщения, используя только 0 или 1? Элементарно! Ведь у нас есть всего две буквы и два значения, поэтому закодировать можно, допустим, так: А = 0, B = 1. Тогда ABBA = 0110, или BBA = 110. Теперь усложним задачу, добавив третью букву — C. Не будем долго думать и предложим такой код: А = 0, B = 1, C = 00. Задача решена? Не совсем. Попробуйте расшифровать вот такое сообщение: 01001. Это может быть АBААB, либо АВCB. Значит, такая кодировка плохая, потому что невозможно расшифровать исходное сообщение однозначно.
А как насчёт такого кода: А = 00, B = 01, C = 11? Попробуем расшифро- вать сообщение 01001101. Разделим все цифры на пары, после чего декодируем каждую:
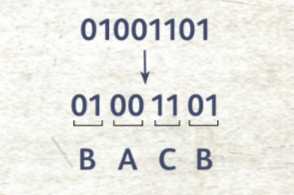
Предложенный код оказался рабочим, но возникла другая проблема. Теперь для кодирования каждой буквы требуется уже два символа, что увеличивает объём в два раза. Рассмотрим английский алфавит из 26 букв. Сколько символов нам нужно, чтобы закодировать все эти буквы? Попробуем обозначить каждую букву 4 символами:

Как видно, 4 символа хватило только на 16 букв, для кодировки остальных мы будем вынуждены повторяться, а это опять вносит неопределённость и делает наш код плохим. Что, если использовать 5 символов? Тогда количество различных вари- антов будет 2×2×2×2×2=32, что больше 26. Следовательно, 5 символов будет достаточно для кодировки 26 букв (на самом деле мы могли бы закодировать даже 32). Заметим, что в этом случае наш исходный текст увеличится уже в пять раз: если мы захотим распечатать, например, «Войну и мир», заменив каждую букву последовательностью из 5 символов, то вместо четырёх томов получим 20.
Первая загвоздка, с которой мы сталкиваемся при кодировании, — это увеличение объёма передаваемого сообщения. Это означает увеличение затрат — времени и энергии — на его передачу. Также из этой проблемы следует другая, более коварная: когда увеличивается объём, растёт и вероятность сделать ошибку.
ПРОБЛЕМА ИСКАЖЕНИЯ
Когда информация передаётся по ка- налу связи, велика возможность её искажения. Вы сталкиваетесь с этим при телефонных разговорах, особенно при использовании стационарных или радиотелефонов. Мы же рассмотрим более простой пример. Предположим, что при передаче кода для каждого символа может исказиться не более одной цифры. Даже это существенно усложняет дело: допустим, мы закодировали А = 00000 и D = 00011, а приняли по каналу связи код 00010. Что это — А с ошибкой в четвёртом символе или D с ошибкой в пятом? Непонятно. Как избежать появления таких ситуаций, да и возможно ли это? Забегая вперёд, от- метим: да, возможно. Но для начала рассмотрим такое решение. Давайте каждую букву будем кодировать не пятью символами, а пятнадцатью, а одну и ту же последовательность из пяти символов запишем трижды. Например, если раньше D кодировался как 00011, то теперь^

Теперь, когда мы получаем на входе пятнадцать символов, их можно разбить на три пятёрки, причём как минимум две из них совпадут, ведь искажение-то могло быть максимум одно! Значит, каждая из этих двух совпавших пятёрок не искажалась, а тогда по любой из них, пользуясь старым кодом из пяти символов, мы можем восстановить исходную букву. Хорошая идея? Не совсем. Вновь возникает проблема увеличения объёма сообщения — «Война и мир» из предыдущего примера разрослась бы уже до 60 томов. А представьте, что нужно передать по сети что-то заведомо большое, например, видеофайл! Но и это ещё не всё. Что, если изменится не один символ, а два или пять?

Контроль четности
Это простейший способ обнаружить одиночную ошиб- ку в передаваемом сообщении. Всё, что нужно сделать, — это к пакету отправляемых данных в конце добавить 1 (если в пакете нечётное число единичек) и 0 (если чётное).

У нас есть 4 единицы, следовательно, контрольное значение должно быть чётным, но там стоит 1. Следовательно, произошла ошибка. Важно отметить, что такой метод не указывает, где именно произошла ошибка, а лишь об- наруживает факт её присутствия.
КОД ХЭММИНГА
Со схожей проблемой столкнулся американский математик Ричард Хэмминг (1915–1998), когда работал в Bell Labs в конце 1940-х. Хэмминг использовал электромеханический компьютер Bell Model V, данные для которого кодировались на специальных листах тонкого картона — перфокартах. Далее эти карты вставлялись в компьютер, а тот считывал информацию. В процессе чтения часто происходили ошибки (искажения), о которых компьютер сообщал оператору. Если последний не реагировал на ошибку (не исправлял программу и не перезапускал её), компьютер продолжал выполнять следующее задание.
Хэмминг часто работал по выходным, когда не было операторов, которые могли бы вручную исправить ошибки. «Чёрт возьми, если машина может обнаружить ошибку, почему она не может определить местонахождение ошибки и исправить её?» — негодовал математик и решил заняться этим вопросом. Уже в 1950 году он опубликовал метод, оказавший существенное влияние на компьютерные науки и телекоммуникации. Суть его метода в следующем: добавим к сообщению несколько контрольных битов (напомним, один бит — это одно место, на которое мы ставим ноль или единицу).
Принимающая сторона повторно вычисляет по тем же формулам контрольные биты и сравнивает их с полученными. Если они совпали — ошибок нет, если не совпали — можно точно найти место, где произошла ошибка, и исправить её. Попробуем разобраться на примере. Чтобы было понятнее, ограничимся не 5, а 4 символами для кодирования, к которым добавим 3 контрольных. Передаваемый блок будет таким:

Грубо говоря, идея в том, что мы смотрим на количество единичных битов среди первых трёх символов, и если это количество чётное, то первый контрольный символ будет равен нулю, а если нечётное, — единице. Аналогично поступаем с остальными двумя контрольными символами (r2 и r3). Наш блок готов к отправке. Будем считать, что он успешно отправлен. Получатель принял наш блок i1i2i3i4r1r2r3 и он должен сделать ещё одну серию расчётов — последовательность синдромов (потерпите совсем чуть-чуть, это последнее непонятное слово):
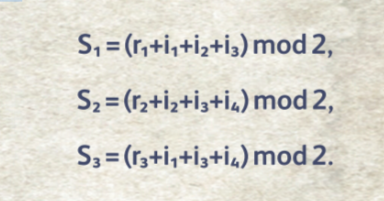
Приглядитесь внимательно. Если никаких искажений не было, то все три синдрома будут равны нулю:
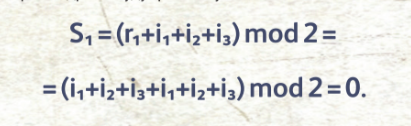
Действительно, если не было искажений, то каждый синдром равен удвоенному соответствующему контрольному символу, взя- тому по модулю два (то есть получается 0, так как чётное число даёт остаток 0 по mod 2). Таким образом, наш алгоритм умеет обнаруживать наличие ошибки. Это ещё не всё. Идём дальше. Допустим, в блоке i1i2i3i4r1r2r3 исказился первый символ i1. Тогда второй синдром не поменяется (S2=0), а первый и третий —изменятся (S1=S3=1). Значит, если записать их подряд, то получаем S1S2S3 = 101. Сделаем аналогичные расчёты для изменений каждого из символов, не забыв и про контрольные, которые тоже могут исказиться:

Отметим, что все последовательности — разные! А значит, мы можем определить, в каком именно символе была ошибка, и исправить её (заменить 0 на 1 или обратно).
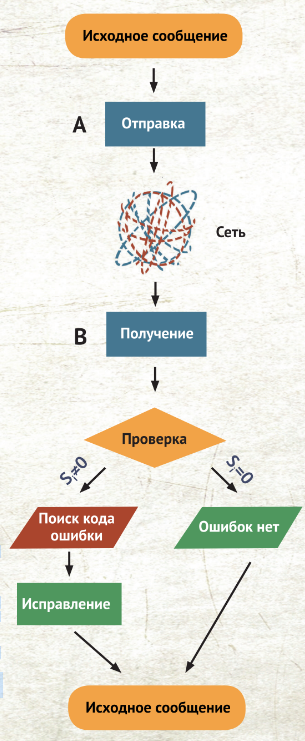
Таким образом, вместо 12 символов (как в примере с добавлением трёх символов к исходной группе из четырёх) мы использовали лишь семь, уменьшив количество символов почти вдвое! И самое главное — код способен самостоятельно исправить ошибку! Схема не сильно усложнится, если исходных символов будет не четыре, а больше.
Можно обобщить код Хэмминга при помощи теории матриц и действий с ними. В такие дебри мы заходить, конечно, не будем. Отметим лишь, что написать программу, которая будет автоматически кодировать, распознавать возможную ошибку и декодировать сообщения сможет каждый.