«Первое слово дороже второго» ,— помнишь детскую дразнилку? Она применима и к цифрам — первая цифра «дороже» второй! Только это уже не дразнилка, а математический закон Бенфорда. Задирать кого-то с его помощью не получится, но обнаружить мошенников очень даже возможно. Так, например, закону Бенфорда нашли применение аудиторские компании. На его основе для целей аудита и выявления случаев мошенничества были построены программные комплексы, с помощью которых за несколько секунд можно обработать массив исходной информации, выявить аномальные результаты и отобрать подозрительные операции для более детальной проверки.

Игры с вероятностью

Возьми шестигранный игральный кубик, на сторонах которого изображены цифры от 1 до 6 — знакомая игральная кость. А теперь бросай. Долго, очень долго, например, 600 раз. И каждый раз записывай, какое число выпало на кубике. Но так уж и быть, не будем заставлять тебя ждать и раскроем секрет сразу. Теория вероятности, о которой мы рассказывали в одном из прошлых номеров, утверждает, что каждое из шести чисел кубика выпадет приблизительно 100 раз (то есть, как говорят математики, вероятность выпадения каждой из цифр равна 1/6). Но чтобы это правило проявилось, нужно бросать кубик многократно (поэтому мы и попросили тебя об этом).

Если бросить его, к примеру, всего шесть раз, то вовсе не факт, что каждая из цифр выпадет всего по разу. А вот если бы ты проделывал это очень долго, то убедился бы, что чем больше бросаешь кубик, тем количество выпадений каждой цифры будет ближе к 1/6 от числа бросков. Но ведь при каждом бросании невозможно точно предсказать, какая выпадет цифра, все выпадения случайны — скажешь ты. Всё правильно, как правильно и то, что многократное бросание кубика подчиняется законам теории вероятности.

В нашем опыте получилось, что вероятность выпадения каждой цифры одинакова, то есть, при бросании шансы выпасть равны для каждой грани кубика. Математики называют такое выпадение цифр равномерным распределением. Только далеко не во всех случайных событиях вероятность одинакова для каждой из цифр: иногда теория вероятности показывает удивительные фокусы.

Потертые страницы

До появления калькуляторов и компьютеров в сложных математических расчётах, например, возведении чисел в степень или извлечении корня, учёные применяли специальные книги-таблицы, которые назывались логарифмическими. Наблюдательный американский астроном Саймон Ньюком в 1881 году обратил внимание на одну странность: те страницы этих библиотечных книг, где числа начинались с единицы, были сильно истрёпаны, а там, где числа начинались на девятку почти нетронуты. Как будто те, кто пользовался таблицами, значительно чаще работали с числами, начинающимися на единицу. Учёный, конечно, понимал, что никакого пристрастия к числам, начинающимся с единицы, ни у его коллег, ни у него самого не было. Правда, никаких выводов из своего наблюдения Ньюком не сделал.

А другой американский учёный — физик Фрэнк Бенфорд в 1938 году решил разобраться с такой особенностью чисел. Для этого он изучил более двадцати разных списков с числами, такими, как: площади бассейнов более 300 рек, численность населения стран, показатели смертности в разных государствах, молекулярные массы около 1800 разных веществ и т. д. По всем показателям Бенфорд составил таблицы, где его интересовала только первая цифра в каждом из чисел. Казалось бы, все эти списки и числа случайны — примерно как результаты бросания кубика, и первая цифра в этих числах должна бы равномерно встречаться от 1 до 9. Но это было не так!

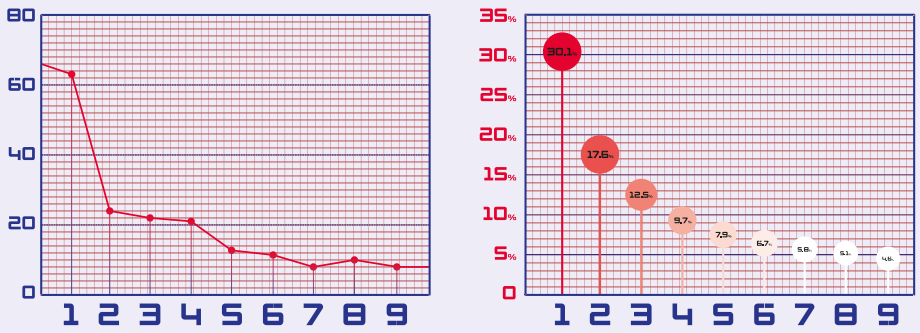
Чисел, начинающихся с единицы, оказалось более 30%, начинающихся с двойки, почти 18%, а те, что начинались с девятки — меньше 5%. Такое распределение чисел учёные называют неравномерным. Учёный составил таблицу, в которой отражено, с какой частотой встречается первая цифра в числах изучаемых им списков.

Непослушные цифры

Очень упрощённо закон Бенфорда объясняется тем, что небольших предметов всегда больше, чем больших. Озёр с небольшой площадью больше, чем крупных, низких сооружений всегда больше, чем высоких, большое количество пострадавших в авариях встречается реже, чем небольшое. А в бухгалтерских операциях чаще встречаются небольшие суммы и реже — крупные.

Конечно, есть у учёных точное математическое обоснование закона Бенфорда, но только при помощи «многоэтажных» формул и специфических терминов. Интересно, что закон первой цифры проявляется на многих списках (таблиц) чисел, хотя и не на всех. Не применим он, к примеру, к списку выигрышных номеров в лото за несколько лет (потому что эти числа не являются размерами чего-то, они случайны так же, как числа при бросании кубика), к списку почтовых индексов или номеров телефонов (потому что первые цифры в этих номерах означают код региона или телефонной станции).

Кроме того, чтобы можно было применить теорию вероятности — обязательно требуется достаточно большой объём таблицы. Так же, как для кубика: если бросишь его несколько раз, то можешь не увидеть как «работает» вероятность, нужно достаточно много бросков, чтобы закон вероятности «проявил себя».

Налоги — в казну!

В 1990-х годах американский математик Марк Нигрини обратил внимание, что закону Бенфорда подчиняются числа в налоговых и бухгалтерских документах. Поэтому он составил специальную программу для проверки налоговых данных. Полезность программы в том, что несоответствие данных закону первой цифры вызывает подозрение в том, что они были кем-то «нарисованы», а не получены естественным расчётным способом (то есть какая-то фирма попыталась исказить суммы налоговых платежей и таким образом укрыться от обязательных выплат государству).

Дело в том, что налоговые службы не могут проверить все компании на правильность уплаты налогов — это физически невозможно из-за очень большого объёма данных. А программа Нигрини даёт возможность, условно говоря, «показать пальцем», какие данные нужно проверять. Это как если бы учитель в школе ещё до начала урока заранее знал, кто вероятнее всего урок не выучил, а потом проверил бы это, вызвав к доске (правда, пока такой программы, к счастью для многих школьников, ещё нет).

К слову, американский математик Марк Нигрини одним из первых использовал закон Бенфорда в аудите и в расследованиях финансовых махинаций. В августе 2014 года он опубликовал статью «Уроки мошенничества в размере 8 миллионов долларов» с Натан Дж. Мюллер, который за четыре года похитил 8,45 миллиона долларов у своего работодателя — страховой компании. В этой статье он привел методы для обнаружения и предотвращения мошенничества в финансовых организациях, за что был удостоен престижной Лоулера за лучшую статью в 2014 году.

Для чего еще используют закона Бенфорда?

C его помощью можно выявлять не только налоговые афёры. Ему подчиняются и данные других бухгалтерских операций. Известен случай, когда предприниматель-мошенник Кевин Лоуренс в США собрал более 90 млн долларов от инвесторов (вкладчиков денег в какой-либо бизнес), якобы на создание сети современных предприятий — клубов здоровья. Но собранные деньги растратил на предметы роскоши для себя и своих дружков, которые уводили средства через подставные компании, при помощи запутанных банковских переводов со счёта на счёт.

Но этому помешал грамотный бухгалтер по имени Даррелл Доррелл. Он проверил более 70 тысяч документов о переводе денег, касающихся подозреваемого предпринимателя, и обнаружил, что данные не соответствуют закону Бенфорда. Так он выяснил, что эти переводы не были «естественными» бухгалтерскими операциями бизнеса. Проверка установила факт мошенничества, и в 2003 году горе-предприниматель был приговорён к двадцати годам лишения свободы.

Практическое задание

Давайте проверим, работает ли закон Бенфорда, например, для данных по численности населения стран. Для этого вам понадобится любой редактор таблиц и данные по численности населения стран (в качестве источника используем Википедию).

Теперь, построим гистограмму данных с последнего столбца (Первая цифра) и сравним с графиком самого закона. Как видите, оба рисунка качественно не сильно отличаются друг от друга. Таким образом вы можете проверить действие закона на любых данных.

Заглавное изображение: news.cgtn.com