Любите ли вы геометрию? Многие на этот вопрос отвечают «нет», потому что в школе
она даётся труднее всего. Причём особенную нелюбовь вызывают у учеников задачи
о пересекающихся отрезках в треугольнике, к которым трудно даже подступиться.
В этой статье мы расскажем о замечательном методе решения подобных задач —
методе масс.
Наверняка в детстве вы качались на качелях-весах. И наверняка один из двоих чаще всего оказывался тяжелее и его сторона постоянно перевешивала. А что можно сделать в этой ситуации, чтобы уравновесить качели?
Вспоминаем правило рычага: чтобы система была в равновесии, моменты сил, действующих на качели, должны быть одинаковыми. Так как силы в нашем случае — это силы тяжести, верно следующее равенство: m1 g l1 = m2 g l2
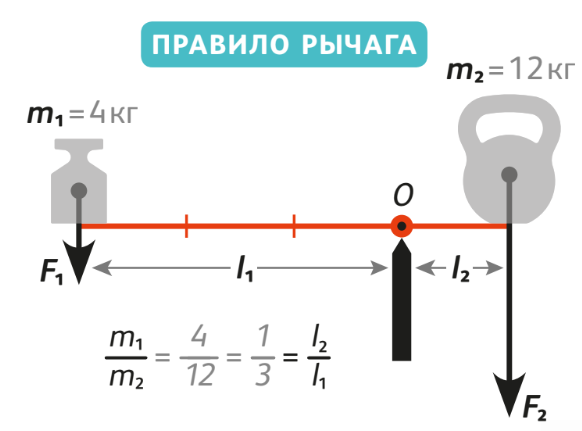
Сокращаем константу g и получаем, что отношение масс обратно пропорционально отношению расстояний от края качелей до опоры:
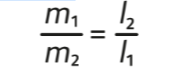
Обратите внимание: вес самих качелей мы не учитываем. То есть система состоит из двух точек — концов отрезка с «гирьками», а также третьей точки, которая делит этот отрезок в отношении, обратно пропорциональном отношению масс «гирек». Последняя точка имеет своё название — она является центром масс системы из двух точек-«гирек».
Центр тяжести
Что же такое центр масс, или, как его ещё называют, центр тяжести? Формальное определение звучит так:
Точка О называется центром масс системы из n точек А1, А2, …, Аn , где каждой точке соответствует масса m1, m2, …, mn , если верно следующее равенство:
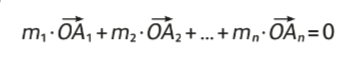
Не пугайтесь этой формулы! На деле решать задачи данным методом можно не думая про векторы. Сделаем допущение, что груз на концах отрезков не имеет размера — только массу. Чтобы найти центр масс системы из двух точек, надо всего лишь разбить отрезок в отношении, обратно пропорциональном массам точек.
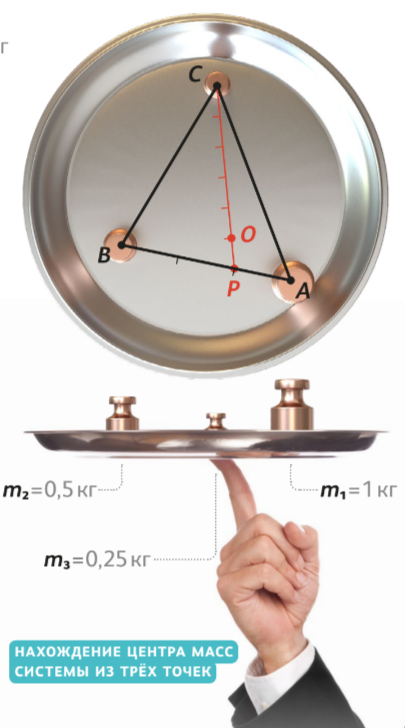
Теперь рассмотрим систему из трёх точек, образующих некий треугольник. Как найти его центр масс? Для большей наглядности представим большой поднос, на котором произвольно расставлены гири. И официанта, который ловко удерживает поднос на одном пальце.
Точка, в которой палец соприкасается с подносом, и есть центр масс. Только условимся, что поднос обладает бесконечно малой массой. Как же найти эту точку? Оказывается, у центра масс есть следующее полезное свойство.
Если есть система точек с массами в них и какую-то пару точек А(mA) и B(mB ) мы заменим их центром масс Р(mA+mB ), то центр масс исходной системы не изменится.
Доказать это свойство попробуйте самостоятельно: это не- сложное упражнение на векторы. Давайте применим указанное свойство к треугольнику. Если есть треугольник с вершинами А, В, С с массами в них, то, чтобы найти центр масс данной системы, можно сперва найти центр масс точек А и В (точку Р), а затем найти центр масс точек Р и С. В каждом из двух случаев центр масс мы находим с помощью обычного правила рычага. Всё это здорово, но возникает резонный вопрос: а зачем? Какое отношение имеют эти рассуждения к геометрическим задачам? Терпение, друзья!
Задача 1
Дан треугольник АВС. М — середина АВ, точка К лежит на отрезке АС и делит его в отношении 1:2 от вершины А. В каком отношении отрезок СМ делит отрезок ВК?
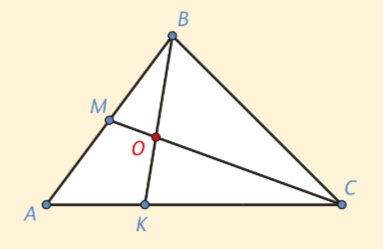
Решение: Суть нашего метода в следующем. Расставим в точки А, В и С массы 2, 2 и 1 соответственно. Как вы видите, центр масс точек А(2) и В(2) — это точка М(4). Значит, центр масс всей системы из трёх точек находится на отрезке СМ и делит его в отношении 1:4 от С. Теперь вернёмся к началу и найдём центр масс точек А и С. Это будет точка К(3). Значит, центр масс исходной системы лежит на отрезке ВК и делит его в отношении 3:2 от В.
Но речь идёт об одной и той же системе точек А, В и С, а значит, у них один и тот же центр масс, который лежит и на СМ, и на ВК. Таким образом, центр масс не что иное, как точка О. Отсюда следует, что искомое отношение ВО к ОК равно 3:2. ОТВЕТ 3:2. Постойте-ка! А как это мы догадались расставить массы именно так: 2, 2 и 1? На самом деле никакой магии тут нет. Наша цель — расставить массы в вершинах треугольника так, чтобы их центром оказалась точка О. Но почему именно 2, 2 и 1?
Всё дело в том, что О будет центром масс, если мы покажем, что центр масс одновременно лежит и на отрезке СМ, и на отрезке ВК. Следовательно, в первом случае массы из точек А и В должны сместиться в точку М. Вспоминаем правило качелей: так как АМ = ВМ, то массы в точки А и В надо ставить одинаковые. Запомним это. Во втором случае мы должны поставить массы в А и С так, чтобы их центром была точка К. Но АК:СК =1:2, значит, в точке А масса должна быть вдвое больше, чем в С.
Следовательно, ставим в С массу 1, тогда в А будет 2 (вдвое больше) и в В — тоже 2 (как в А). Методом масс можно не только решать задачи, но и доказывать теоремы.
Задача 2
Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин.
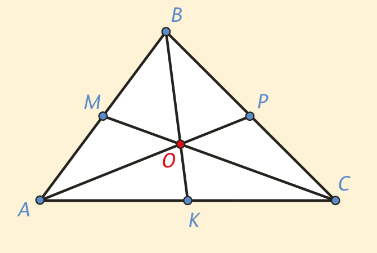
Решение: Рассмотрим медианы ВК и СМ. В данном случае и К, и М — середины, поэтому поставим во все три вершины А, В и С массу 1. Далее рассмотрим точки А и В. Их центр масс — точка М(2). Значит, центр масс системы точек А, В и С лежит на отрезке СМ и делит его в отношении 2:1 от вершины С. Теперь рассмотрим точки А и С, их центр масс — точка К(2). Значит, центр масс всё той же системы точек А, В и С лежит на отрезке ВК и делит его в отношении 2:1 от вершины В.
Но тогда искомый центр масс — это точка О на пересечении отрезков ВК и СМ, причём каждый из отрезков эта точка делит в отношении 2:1 от вершин. Осталось заметить, что если мы рассмотрим медианы ВК и АР, то их точка пересечения также будет центром масс и разделит ВК и АР в отношении 2:1 от вершин. Но точка, которая делит ВК в отношении 2:1 от В, единственная, значит, в обоих случаях речь идёт об одной и той же точке О. Итак, все три медианы проходят через точку О и делятся ею в отношении 2:1 от вершин, что и требовалось доказать.
В заключение хочется отметить, что мы рассмотрели лишь некоторые способы применения этого интереснейшего метода. Опробуйте его сами в аналогичных задачах и оцените лёгкость и элегантность решений!






