КИТАЙЦЫ НА КАРТЕ
В Китае проживает более миллиарда человек. Казалось бы, если карта Китая уменьшена в масштабе 1 : 1 000 000 (в 1 см 10 км) к реальной территории страны, то на ней должно поместиться и пропорциональное количество жителей — не менее 1000 человек. Но вы навряд ли уместите на ней даже 50! Посчитайте сами, Китай простирается примерно на 5 250 км с востока на запад и на 5 500 км с севера на юг, значит, при масштабировании наша карта будет всего 5,2 × 5,5 метров — маловато для 50 человек. Можете ли вы объяснить это противоречие? Уменьшили в миллион раз и карту, и количество, а противоречие очевидно. Как так получается? Чтобы понять, давайте разберём простой пример. Каждую из сторон прямоугольника уменьшили в два раза. Во сколько раз уменьшилась его площадь?
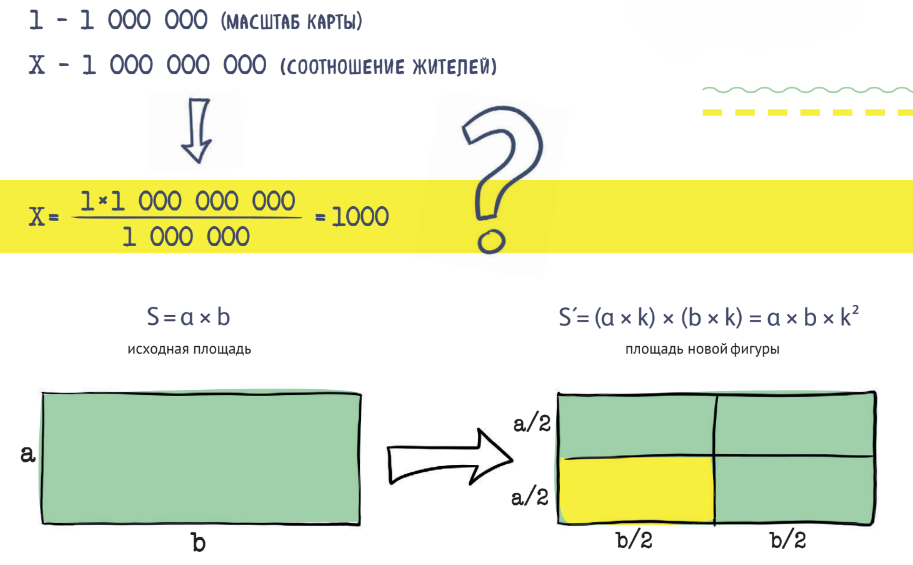
Конечно, не в два, а в четыре. Действительно: если каждая сторона уменьшилась в два раза, то, вычисляя площадь, мы вдвое уменьшаем каждый из двух множителей, следовательно, произведение уменьшится уже в четыре раза. А что было бы, если бы мы уменьшили каждую сторону в три раза? Площадь уменьши- лась бы в девять раз. Решение в общем виде выглядит так: если мы изменили каждую сторону в k раз (обе увеличили или обе уменьшили), то площадь изменится в k2 раз — соответственно, увеличится или уменьшится.
Этот вывод верен для любой плоской фигуры. Попробуйте убедиться в этом сами. Теперь вернёмся к картам и Китаю. Когда мы рассуждаем о том, сколько человек поместится на карте, мы подразумева- ем занимаемую ими площадь. А ведь площадь карты меньше площади Китая не в миллион, а в миллион в квадрате, то есть в триллион раз! Поэтому наш первоначальный вывод и неверен.
МЫЛО И ОБЪЁМЫ
Рассмотрим простой пример, который нередко предлагают на школьных олимпиадах или во время собеседования на работу. Кусок мыла, имеющий форму прямоугольного параллелепипеда, после семи стирок уменьшился в два раза по всем трём измерениям. На сколько стирок хватит оставшегося куска мыла? Интуитивно хочется дать быстрый ответ — на семь. Вроде бы логично, уменьшился кусок в два раза (то есть наполовину), значит, на столько же ещё и хватит. Это рассуждение — неверное. Доказать это можно простым и сложным способами. Для сложного доказательства нам потребуются формулы. Предположим, что за каждую стирку тратится одинаковый объём мыла вплоть до седьмой стирки.

Для простого доказательства нам потребуется изображение прямоугольного параллелепипеда. Разделим наш исходный кусок мыла на равные части по всем трём измерениям. Получим восемь равных кусочков, из которых после семи стирок останется лишь один. Но тогда за семь стирок было потрачено семь кусочков, а значит, одного кусочка хватает ровно на одну стирку. Вывод аналогичен выводу в истории с площадью: когда фигура масштабируется в х раз, её объём изменяется в х3 раз. Кстати, если объект однороден, то точно так же изменяется и его масса. И иногда это бывает очень важно. Смотрите сами.
СЛУЧАЙ НА СКЛАДЕ
Грузчик на складе может поднять упаковку размером 3 × 3 × 3 литровых пакета молока. Смогут ли три грузчика поднять упаковку из 9 × 9 × 9 пакетов? Во-первых, убедимся, что условие задачи правдоподобно: упаковка 3 × 3 × 3 содержит 27 пакетов, которые весят в сумме примерно 27 килограммов. Конечно, такую упаковку взрослый человек поднимет без труда. Что ж, теперь «утроим» задачу. Пришло втрое больше людей, взяли в три раза больше молока — вроде бы опять логично. Но нет! Действительно, если мы увеличили каждое измерение в три раза, то и объём — а значит, и масса — увеличится в 27 раз! То есть нам потребуются целых 27 грузчиков, ведь трём людям поднять 729 килограммов будет невероятно сложно.
СЛОНЫ И СЛОНЯТА
В зоопарке живут взрослый слон и маленький слонёнок. Слон больше слонёнка в два раза по каждому измерению. Считая, что количество корма для слона пропорционально его весу независимо от возраста, во сколько раз больше корма должен получать взрослый слон по сравнению со слонёнком?
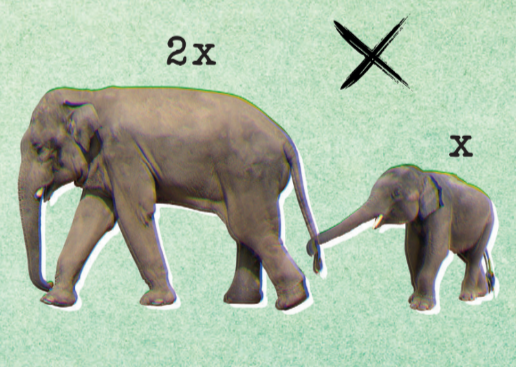
Опять же, напрашивается ответ «вдвое больше». Увы, если мы поступим таким образом, бедный взрослый слон начнёт быстро худеть. Действительно, как мы уже знаем, при масштабировании слона в два раза объём увеличится в восемь раз, а значит, масса — тоже (на самом деле, конечно, слоны неодно- родны, так что вряд ли ровно в восемь, но порядок будет при- мерно такой). Так что и корма надо давать не в два раза больше, а в восемь!
Эх, как грустно жилось бы слону, не проходи служители зоопарка тему «Объёмы» в школе! Кстати, небольшой контрольный вопрос: если сфотографировать слона и слонёнка, то во сколько раз площадь слона на фотографии будет больше площади слонёнка? Правильно, в четыре раза, это же площадь!

ПОСРАВНИВАЕМ?
Две кастрюли имеют форму цилиндра, но первая в два раза выше, а вторая — в два раза шире. Какая кастрюля более вместительна? Сперва вспомним формулу объёма цилиндра: V=πR2h. Обратите внимание на то, как изменяются радиус и высота в этой формуле. Изменение радиуса, очевидно, имеет большое влияние на объём. Высота второй кастрюли в 2 раза меньше, но радиус основания в 2 раза больше, а значит, площадь основания больше в 4 раза. Таким образом, вторая кастрюля вместительнее (причём ровно в два раза).
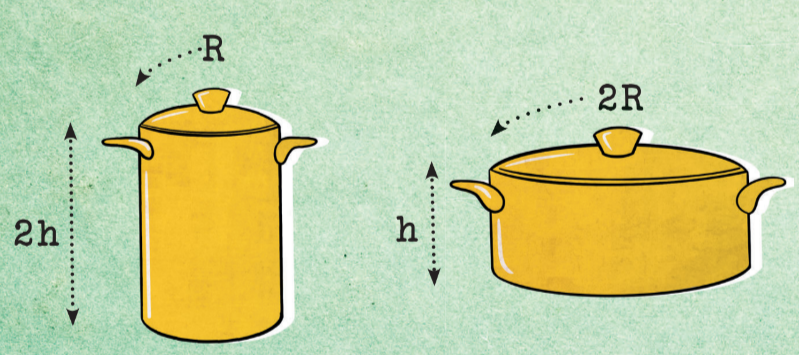
Кстати, если от нас не требуется понять, во сколько раз объём второй кастрюли превышает объём первой, то сравнить их можно и проще. Давайте «распилим» первую кастрюлю пополам парал- лельно основанию. Получим две кастрюли поменьше (к слову, одна из них — без дна), которые легко поместятся во второй ка- стрюле: если мы поставим их рядом, то они как раз влезут, и даже останется много свободного места. Так что и без формул можно увидеть, что вторая кастрюля более вместительная.
И ПОВЗВЕШИВАЕМ
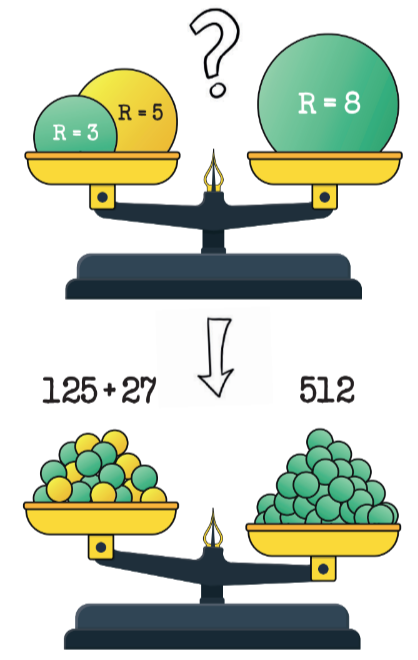
На левую чашу весов положили два шарика радиусом 3 см и 5 см соответственно, а на правую чашу — шарик радиусом 8 см. Все три шарика сделаны из одинакового материала и не содержат полостей внутри. Какая чаша весов перевесит? И снова, возможно, интуиция предлагает ответ: «Никакая». Действительно, 3 + 5 = 8! Однако не будем торопиться, а попробуем немного посчитать. В принципе, можно воспользоваться формулой объёма шара, но давайте ограничимся более примитивным, но не менее верным рассуждением.
Рассмотрим шарик единичного радиуса. Когда мы увеличиваем радиус втрое, то объём, а значит, и масса, вырастут в 27 раз (33). Стало быть, вместо шарика радиусом 3 см можно рассмотреть 27 шариков радиусом 1 см. Аналогично, вместо шарика радиусом 5 см рассмотрим 125 (53) шариков радиусом 1 см, а вместо шарика на правой чаше весов — 512 (83) шариков радиусом 1 см. Несложно убедиться, что правая чаша перевесит — и очень существенно. Заметьте, что даже четыре 5-сантиметровых шарика не перевесят один 8-сантиметровый, так как 500 < 512. Мистика? Магия? Нет, математика!
НА ДЕСЕРТ
Арбуз имеет форму шара. Снаружи он покрыт коркой, причём толщина корки в три раза меньше радиуса мякоти. Во сколько раз объём мякоти превышает объём корки? Прежде чем решить этот пример, попробуйте угадать ответ! Кто-то говорит: в три раза. Кто-то выбирает ответ 27. Часть опрашиваемых скажет «9». Некоторые останавливаются на 2 или 1,5. А кто из них прав? Конечно, никто! И сейчас мы в этом убедимся. Давайте рассмотрим арбуз как идеальный шар. Пусть радиус корки равен х.

Тогда по условию радиус мякоти — 3х, а радиус всего арбуза — 4х. Как мы помним из предыдущей задачи, шар радиусом 3х можно рассматривать как 27 шариков радиусом х (эти 27 ша- риков приходятся на мякоть). Значит, весь арбуз (радиусом 4х) — это 64 шарика радиусом х. Стало быть, если принять объём маленького шарика за 1, то объём арбуза равен 64, а объём мякоти — 27. Но тогда на корку приходится 64 − 27 = 37, так что объём мякоти не просто не в три и не в два раза больше: он вообще меньше объёма корки! Спасибо, логика, что ты с нами!






