В математике, прежде чем использовать какую-либо теорему, её нужно доказать. Процесс этот многим кажется скучным: долгие рассуждения с множеством терминов, отсылки на другие теоремы… Попробуй всё это удержать в голове! Вот бы было так, что смотришь на доказательство и сразу всё понятно! Как-то египетский царь Птолемей попросил Евклида быстро объяснить ему все науки. «Царской дороги в геометрии нет!» — кратко изрёк тогда Евклид. Но в некоторых теоремах «царский», лёгкий путь доказательства действительно существует — достаточно одного рисунка.

ТЕОРЕМА ВИВИАНИ

Если внутри равностороннего треугольника отметить точку, то сумма расстояний от неё до сторон треугольника постоянна и равна высоте треугольника.

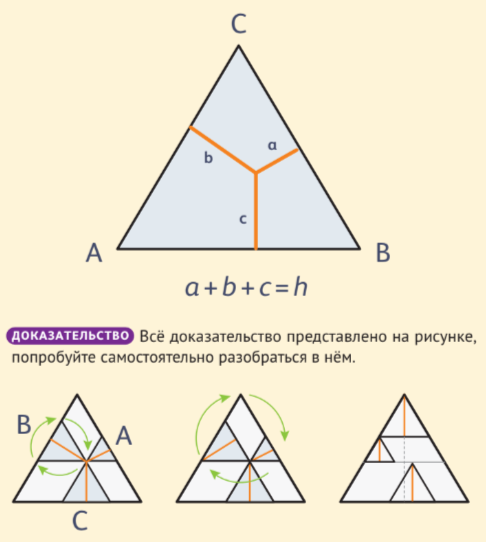
ПОЯСНЕНИЕ К ДОКАЗАТЕЛЬСТВУ

Сперва на исходных отрезках (a, b, c) построим равносторонние треугольники (A, B, C). Развернём равносторонний треугольник B вокруг его центральной оси на 120 °. Теперь развернём на тот же угол равносторонний треугольник, в который входят B и А, вокруг его центральной оси. Видно, что высота исходного треугольника равна сумме высот маленьких треугольников.

ТЕОРЕМА НИКОМАХА

Сумма кубов последовательности натуральных чисел равна квадрату их суммы:

1³ + 2³ + 3³ + 4³ +…+ n³ =
= ( 1 + 2 + 3 + 4 +…+ n)²

ПОЯСНЕНИЕ К ДОКАЗАТЕЛЬСТВУ

Обратите внимание на то, что паттерн рисунка повторяется у чётных и нечётных n. Давайте проверим теорему для n=2:

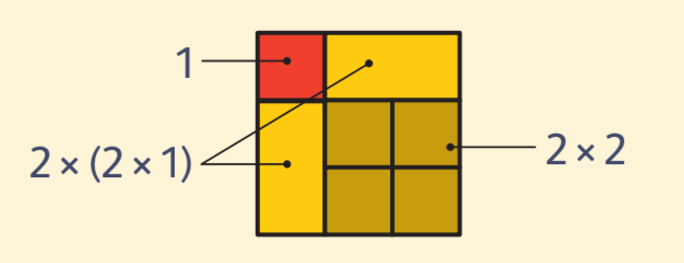
S = 1³ + 2 × 2² = 1³ + 2³ = 9 = (1 + 2)²

Теперь проверим для n=3:

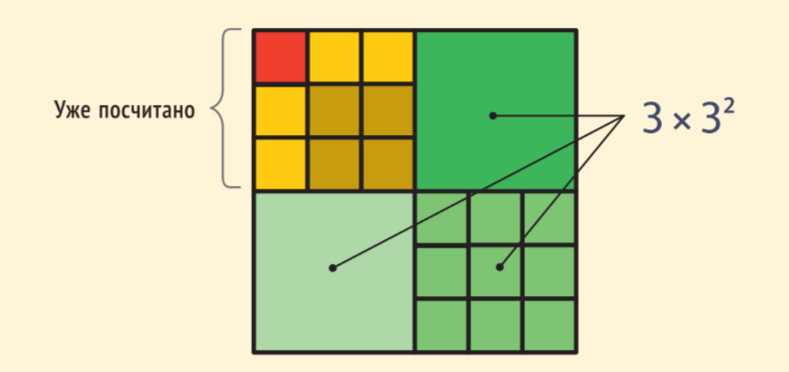
S = 1³ + 2 × 2²+ 3 × 3²=1³+ 2³ + 3³ = 36 = (1 + 2 + 3)²

ТЕОРЕМА О СУММАХ НЕЧЁТНЫХ ЧИСЕЛ

Сумма n нечётных натуральных чисел равна их квадрату:

S = 1 + 3 + 5 +…+ ( 2n − 1) = n²

ПОЯСНЕНИЕ К ДОКАЗАТЕЛЬСТВУ
Обратите внимание на то, что при подобном расположении длина каждого последующего слоя больше на 2, а начинается всё с 1. У нас есть два способа подсчитать количество элементов
в квадрате: возвести его сторону в степень 2 или сложить слои, из которых он состоит.

ТЕОРЕМА О СУММЕ РЯДА НАТУРАЛЬНЫХ ЧИСЕЛ

Сумма первых n натуральных чисел равна:

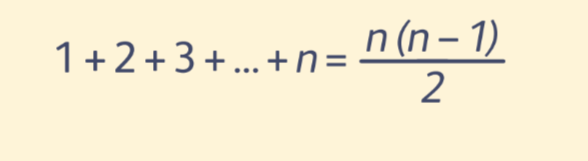
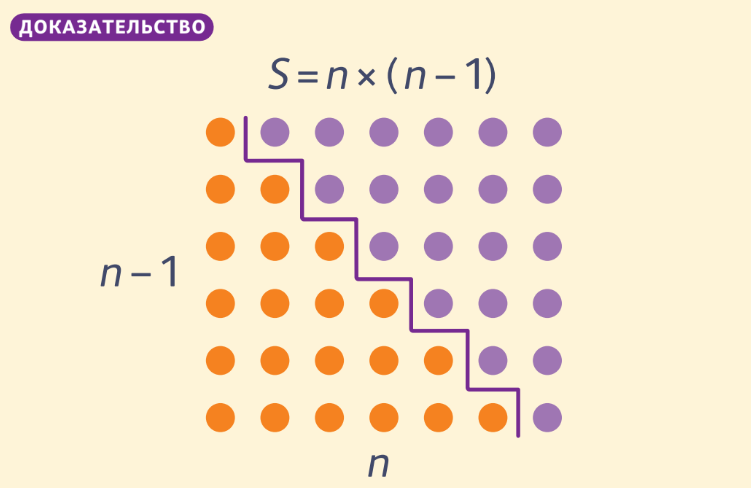
ПОЯСНЕНИЕ К ДОКАЗАТЕЛЬСТВУ
Нижняя «лесенка» шариков есть искомая сумма. Если дополнить её точно такой же перевёрнутой «лесенкой», получим прямоугольник, площадь которого равна произведению сторон. Осталось только разделить эту площадь пополам.

ТЕОРЕМА О ПЛОЩАДИ КРУГА

Площадь круга равна произведению квадрата радиуса на число π:

ПОЯСНЕНИЕ К ДОКАЗАТЕЛЬСТВУ
Разрезая окружность на более мелкие секторы и собирая их попарно вместе, можно получить прямоугольник. Его площадь равна площади исходного круга и определяется как произведение его сторон.

Заглавное изображение: Unsplash