При решении математических задач может случиться так, что некоторые переменные или их свойства не меняются. Если суметь разглядеть эти свойства, они могут стать ключом к решению. Мы научим вас искать инварианты — так в математике принято называть нечто неизменяемое. Помогут нам в этом герои «Игры престолов». Валар моргулис! Не бойтесь, спойлеров не будет.

Забегая немного вперед, отметим что инварианты полезны для решения математических задач, так как они помогают:

• Сравнивать объекты. Если инварианты двух объектов различаются, это значит, что объекты тоже разные.
• Упрощать вычисления. Иногда легче анализировать инварианты, чем сам объект.
• Систематизировать и классифицировать объекты. Например, инварианты помогают классифицировать многообразия или дифференциальные уравнения.

Инварианты находят применение не только в математике, но и в физике, информатике, экономике и других cферах.

НЕМНОГО ТЕОРИИ

Инварианты в математике — это величины или свойства, которые остаются неизменными при определённых преобразованиях объектов. Другими словами, инвариант — это характеристика объекта, которая не меняется при изменении каких-либо его параметров или при применении к нему определённых операций.

Начнём с примера. Допустим, что у модницы Серсеи из книги Джорджа Мартина есть шкаф, который вмещает только 1000 платьев, и каждый раз, когда она покупает новое платье, ей приходится выкидывать одно старое. И наоборот: когда она выкидывает старое — тут же должна купить новое. Может ли так случиться, что у неё когда-нибудь окажется 1002 платья в шкафу? Разу- меется, нет. Ведь количество платьев в шкафу — величина, которая остаётся неизменной. Конечно, это был простой пример. Но сам принцип поиска неизменных величин помогает решать более сложные задачи. В математике такие величины называют инвариантами.

НЕИЗМЕННАЯ ЧЁТНОСТЬ

Один из часто встречающихся инвариантов связан с чётностью. В некоторых задачах величина может непредсказуемо меняться, но не менять при этом своей чётности. Вот несколько примеров с таким инвариантом?

ПРИМЕР 1
В первом сезоне «Игры престолов» было 11 главных героев. В каждом сезоне Джордж Мартин вводит 2, 4 или 6 новых персонажей и убивает 2, 4, 6 или 8 героев. Может ли к концу сериала Железный трон достаться двум выжившим?

РЕШЕНИЕ

Заметим, что добавление и вычитание чётных чисел не меняет чётности исходного числа. Значит, количество главных героев после любого сезона будет оставаться нечётным, так как оно было нечётным изначально. То есть нечётность количества главных героев инвариантна в течение всего сериала. А итоговое число 2 — чётное. Мы обнаружили противоречие. Значит, невозможно, чтобы Железный трон поделили двое. Обратите внимание, что неизменна только чётность в количестве героев, а их общее число может меняться.

Заметим, что добавление и вычитание чётных чисел не меняет чётности исходного числа. Значит, количество главных героев после любого сезона будет оставаться нечётным, так как оно было нечётным изначально. То есть нечётность количества главных героев инвариантна в течение всего сериала. А итоговое число 2 — чётное. Мы обнаружили противоречие. Значит, невозможно, чтобы Железный трон поделили двое. Обратите внимание, что неизменна только чётность в количестве героев, а их общее число может меняться.

ПРИМЕР 2

Лорды и леди Семи Королевств решили выбрать правителя голосованием. Есть 6 кандидатов. Каждый голосующий отдаёт ровно 2 голоса — по одному за каждого из двух выбранных им кандидатов. После того, как Тирион подсчитал голоса, он заявил, что 5 кандидатов набрали равное количество голосов, а Арья Старк – на 1 голос больше остальных. Докажите, что Тирион оказался неправ.

РЕШЕНИЕ

Где же тут инвариант? 2 голоса и 6 кандидатов намекают нам на чётность. Но на чётность чего? На чётность количества набранных одним кандидатом голосов? Нет, ведь он может набрать как чётное, так нечётное количество голосов.

А вот чётность общего количества голосов не меняется. Если каждый выбирающий должен отдать 2 голоса, то общее количество голосов всегда будет чётным — 12. А что мы получили, по словам
Тириона? Все 6 кандидатов набрали одинаковое количество голосов, то есть общее количество голосов кратно 6. Значит, оно чётное. Но «лишний» голос за Арью нарушает необходимую
чётность. Значит, Тирион обсчитался. Намеренно или нет — мы не знаем. Но Север, конечно же, всё помнит.

ПРИМЕР 3

Королева Серсея приговорила Тириона к смерти, но после заступничества Джона Сноу решила дать деснице шанс. Она предложила ему сыграть в игру: на столе стоят 6 кубков, из них 1 стоит дном вверх, а остальные — дном вниз. За ход можно перевернуть любые 2 кубка. Если Тирион сможет перевернуть все кубки дном вверх, то его освободят. Сможет ли Тирион спастись?

Увы, пока мы лишь осознали, что именно такая последовательность действий к успеху не приведёт. Но, может, мы просто неправильно действовали? На помощь приходит идея с инвариантами, благодаря которой мы можем доказать, что выиграть в эту игру невозможно. Ведь коварная Серсея могла выставить 10 000 кубков, тогда обман для нас был бы не так очевиден.

РЕШЕНИЕ

В начале игры дном вверх стоял только 1 кубок. За ход мы переворачиваем 2 кубка либо вверх дном (тогда количество кубков, стоящих вверх дном, увеличивается на 2), либо вниз дном (количество кубков, стоящих вверх дном, уменьшается на 2), либо переворачиваем 2 разных кубка (они, по сути, меняются местами, а значит, количество кубков, стоящих вверх дном, не изменится). Итак, количество кубков, стоящих вверх дном, может как увеличиться на 2, так и уменьшиться на 2, либо остаться без изменений. А тогда чётность количества кубков, стоящих дном вверх, не изменяется. Вот он, инвариант!

Осталось заметить, что в начале игры количество кубков, стоящих дном вверх, было нечётным (1 кубок), а в искомой расстановке оно чётное (6 кубков). Значит, выиграть невозможно, к несчастью для Тириона. Как видите, инвариант не всегда лежит на поверхности, но нередко он связан с чётностью.

ДРУГИЕ ИНВАРИАНТЫ

ПРИМЕР 4

Ходор придумал собственный язык, в котором используются только буквы Д и Р. Словом он считает любую последовательность Д и Р. Известно, что смысл слова не изменится, если из него убрать повторяющиеся буквы Д и Р (ДДДРРР = ДР), а также при добавлении в любое место слова буквосочетания РД или РРДД. Можно ли утверждать, что слова РДД и ДРР имеют одинаковый смысл?

РЕШЕНИЕ

Если переформулировать задачу, вопрос в ней таков: можно ли получить слово ДРР, добавляя в любое место слова РДД такие буквосочетания как РД и РРДД? Для начала попробуем поменять что-нибудь по этим правилам.

Например:

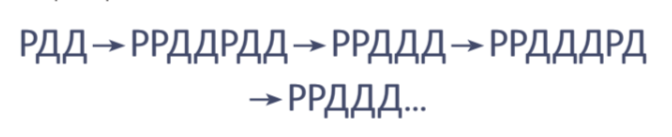
Сходу не очень получается. Однако это, конечно, не доказательство. Вдруг сейчас у нас не получилось, но получится с другим вариантом решения?

Вторая идея приходит по инерции. Чётность! Несложно видеть, что мы добавляем или убираем чётное количество букв. Значит, чётность общего количества букв в словах, имеющих одинаковый смысл, — инвариант. Но вот беда: оба искомых слова имеют по три буквы, так что этот инвариант нам не поможет. Если присмотреться к буквосочетаниям РД, РРДД и ДР, можно понять, что в каждом из этих «кусочков» поровну букв Р и Д. Но тогда добавляй эти «кусочки» или убирай — разница между количеством букв Р и Д в слове будет одинаковой! Вот он, новый инвариант. В исходном слове РДД букв Д на одну больше, значит, их и всегда будет на одну больше, и слово ДРР мы получить не сможем. Задача решена! И безо всякой чётности.

ПРИМЕР 5

5 Санса, Мирцелла и Маргери захотели выяснить, кто из них умнее. Для этого они начали решать задачи. Девушки договорились, что за каждую решённую задачу та, кто решит её первой, получает 4 золотых монеты, решившая второй — 2, а решившая последней — 1. Девушки говорят, что каждая из них решила все задачи и получила 20 монет, причём одновременных решений не было. Может ли такое быть?

РЕШЕНИЕ

Попробуем поискать здесь чётность. Возможно, речь об общем количестве монет? Мы его, конечно, исходно не знаем, но можем подсчитать: каждая получила по 20 монет. Значит, всего у них 60 монет. Чётное количество. С другой стороны, за каждую задачу они получили в сумме 7 монет (4 + 2 + 1) — нечётное количество. Но, увы, пока противоречия не намечается: если задач было чётное количество, то, взяв 7 чётное число раз, мы получим чётную сумму. Кстати, если бы числа были чуть другими (например, по 21 монете у каждой, и первая получает не 4 монеты, а 5), то чётность бы сработала.

Действительно, в этом случае каждая задача приносит чётное число монет (5 + 2 + 1), а тогда независимо от количества задач общее число полученных монет будет чётным. Но оно же равно 63, то есть нечётному числу. Да, чётность как инвариант не сработала. Но зато теперь стало понятно, что общее число монет должно делиться на 7! Действительно, если каждая задача приносит по 7 монет, то независимо от количества задач число полученных монет всегда делится на 7. А 60 на 7 не делится. Значит, героини нашей задачи пока не научились считать достаточно хорошо… Что же здесь было инвариантом? Например, остаток от деления количества монет на 7 — он всегда равен нулю, и не важно, сколько задач было решено.

ПРИМЕР 6

В Королевской Гавани живет 17 шпионов Серсеи, 15 шпионов Дейенерис и 13 шпионов Джона Сноу.

Общее количество шпионов – это инвариант (их 45). Но в решении это не поможет. Чётность шпионов каждого правителя меняется, если его шпион уходит к другому. А вот разница меняется определённым образом. Исходно у Джона было на 4 шпиона меньше, чем у Серсеи. Если встретились шпионы Серсеи и Джона, то разница не изменилась. Если встретились шпионы Серсеи и Дейенерис, то разница изменилась на 3 в пользу Джона (у него прибавилось 2, а у Серсеи стало меньше на 1). Аналогично при встрече шпионов Джона и Дейенерис разница между количеством шпионов у Серсеи и Джона изменилась на 3, но теперь уже в пользу Серсеи. Разница, которая была равна 4, либо не меняется, либо меняется на 3 в ту или другую сторону. Однако тогда остаток от деления этой разницы на 3 — инвариант! Он всё время равен 1. А если бы все шпионы служили одному правителю, то разница была бы либо 0 (если этот правитель — Дейенерис), либо 45. В обоих случаях остаток при делении на 3 равен 0, а значит, такое невозможно.