Лишь математики увидят в таком вопросе смысл. Более того, они находят вполне логичный на него ответ. Хотите узнать, сколько элементов в бесконеч- ности и какими свойствами они обла- дают? Сегодня мы поговорим об одном из самых умопомрачительных разделов математики — теории множеств.
ЧТО ТАКОЕ МНОЖЕСТВО?
Множество — это совокупность элементов, обладающих каким-либо общим свойством. Элемент ом может быть что угодно: фрукты, машины, люстры, люди… Например, книжный шкаф — это множество. В нём содержатся разные элементы (например, книги, открытки и статуэтки), а общее их свойство заключается в том, что все они находятся на полках именно этого шкафа. Обратите внимание, что предметы могут быть какими угодно, главное, что у них есть общий атрибут. Теперь рассмотрим некоторое числовое множество, то есть его элементами будут числа:
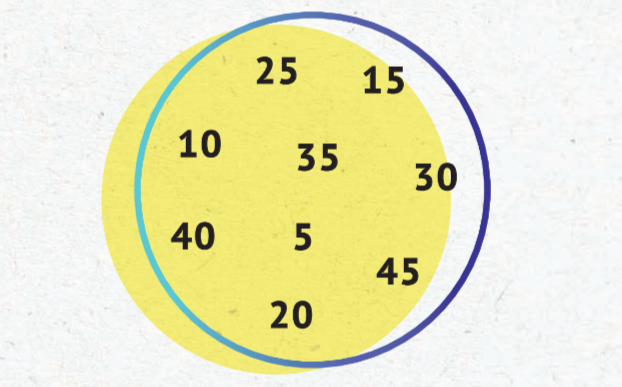
Общий атрибут — признак делимости на 5. Но каждый раз зарисовывать множества неудобно, поэтому в математике их записывают следующим образом: X= {5, 10, 20, 15, 25, 30, 35, 40, 45}, где название всегда обозначают заглавной латинской буквой. Но это же множество можно описать, а не пе- речислять все его элементы. Например: X = {a, где a ∈ N, a ≤ 45 и a mod 5 = 0}, т. е. натуральные числа, меньшие или равные 45 и кратные 5. Если объект a является элементом множества X, это записывается так: a ∈ X. Например, 1 ∈ {1, 2, 3}.

ЭЛЕМЕНТЫ МНОЖЕСТВА
Объединить по общему свойству можно что угодно. Например, множество писателей ростом ниже 165 см или множество цветов, передаваемых монитором и т.д. Эти множества конечны. В математике это означает, что вы можете пересчитать элементы и получить точное их число, даже если их невероятно много. Например, конечны множества птиц, песчинок на пляже, волос на голове, звёзд во Вселенной… Теоретически, можно придумать способ их пересчитать. Если есть конечные, значит, существуют и бесконечные? Да, это так. Элементы в них невозможно подсчитать. Например, множество всех натуральных чисел: допустим, вы назовёте «самое большое число», но всегда к нему можно прибавить единицу, а потом ещё и ещё. Для сравнения множеств в математике существует понятие мощности. Она определяется количеством уникальных элементов. Например, мощность множества {ручка, карандаш} равна 2 и мощность {ручка, карандаш, ручка, ручка, карандаш} будет тоже равна 2. У бесконечного множества мощность равна бесконечности.

Но вы можете сравнивать множества и более наглядным образом, соединяя их элементы попарно — то есть мы берём один элемент из первого множества и сопоставляем ему единственный из элементов второго множества. Тогда два множества {ручка, карандаш} и {тетрадь, книга} можно сравнить так: ручка — тетрадь и карандаш — книга. Несопоставленных элементов не осталось, значит, мощности множеств совпадают. Порядок не имеет значения. А мощности множеств {яблоко, груша, ананас} и {7, 8} различаются — при сопоставлении всегда останется один лишний фрукт.

РАВЕНСТВО МНОЖЕСТВ
Есть ли у множеств {черепаха, мышь, голубь, рыба, улитка} и {1, 2, 3, 4, 5} общие элементы? Нет, поэтому они называются непересекающимися (независимыми). Вот ещё один пример таких множеств: {1, 2, 3} и {4, 5, 6}. Иногда у элементов можно обнаружить дополнительные общие свойства и на их основе составить подмножество. Например, среди множества плодов могут образоваться подмножества жёлтых и красных плодов.

Рассмотрим два множества: A = {a, b, с} и B = {a, b, c, d}. Все элементы A также находятся в B. В таких случаях говорят, что A является подмножеством B , и записывают A ⊆ B (читается как «А содержится в В»). Зная всё это, мы наконец можем дать определение равным множествам — они имеют одинаковую мощность и состоят из одних и тех же элементов, то есть все элементы одного набора принадлежат другому и наоборот. Например, в книге о волшебнике Гарри Поттере множество букв имени одного из героев романа «Tom Marvolo Riddle» равно множеству букв фразы «I am Lord Voldemort» («Я Волан-де-Морт»):

Нетрудно заметить, что A и B состоят из одного и того же множества букв {t, o, m, a, r, v, l, i, d, e}, следовательно, A и B являются подмножествами друг друга, а значит, равны между собой.
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
Два множества могут отличаются друг от друга по признакам, но иметь общие элементы, которые называют пересечением. Рассмотрим классическую задачу. На прогулке 2 отца и 2 сына нашли три апельсина, каждому досталось по одному апельсину — как такое возможно? Такое реально, если речь идёт о дедушке, сыне и внуке. Множества отцов и сыновей «пересекаются» на отце внука или на сыне дедушки (это один и тот же человек).
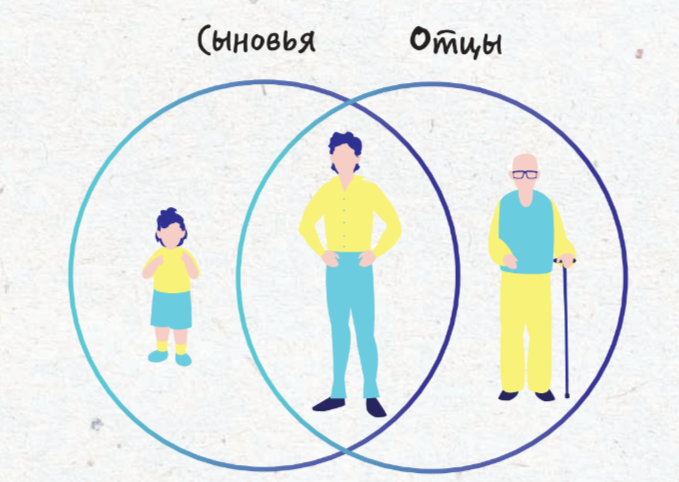
Другой пример. Возьмём множества чисел, кратных 5 и 3: А = {10, 15, 20, 25, 30, 35, 40, 45} и B= {3, 9, 12, 15, 18, …, 30, 45} соответственно. Среди этих чисел те, которые делятся и на 3, и на 5, обра- зуют пересечение A и B. Математически это обозначается так: A ∩ B = {15, 30, 45}.

ОБЪЕДИНЕНИЕ МНОЖЕСТВ
Объединение двух или более множеств включает в себя все элементы исходных множеств. Например, если вы возьмёте бинокль и закроете один из окуляров, вы получите одно изображение (множество А). Если повторите это со вторым окуляром, получите второе изображение (множество В).

Возвратимся к задаче с кратными числами: объединением в таком случае будут числа, которые делятся либо на 3, либо на 5, либо на 3 и на 5 одновременно. Математически объединение обозначается так: A ∪ B = {3, 6, 9, …, 40, 45}. Это основные операции, которые вы должны знать о множествах и которые нам понадобятся далее.

СРАВНИВАЯ БЕСКОНЕЧНОСТИ
Рассмотрим бесконечное множество целых чисел A = {1, 2, 3, …} и его подмножество B = {4, 8, 12, …} — целые числа, кратные 4. Напомним, что количество элементов A и B бесконечно: если вы назовёте самое большое целое число (или число, кратное 4), то, прибавив к нему 1 (или 4), мы получим следующий элемент множества, и так бесконечно долго. Вроде бы очевидно, что чисел, кратных 4, должно быть меньше, чем чисел вообще. Интуиция рисует перед нами следующую числовую прямую и подсказывает, что часть не может равняться целому.
Но в математике эти бесконечные множества имеют одинаковую мощность, то есть чисел, кратных 4, столько же, сколько всего целых чисел (!). Как это доказать? Пересчитать все элементы напрямую мы не можем (ведь их бесконечное количество). Как быть? Поступим, как в известной задаче, в которой надо определить, хватает ли стульев гостям в комнате. Её решение очень простое: нужно попросить гостей занять свободные стулья. Так мы попытаемся установить взаимно однозначное соответствие между людьми и стульями, объединяя их в пары человек — стул. При этом нет надобности пересчитывать стулья и гостей, наша задача — придумать способ их соотнести между собой. Поэтому если мы сможем каждому элементу множества A сопоставить один элемент множества B, то можно утверждать, что количество элементов совпадает.
Представим множество целых чисел: A = {1, 2, 3, 4, 5, 6, 7, …}. Теперь каждый элемент множества умножим на 4 и получим новое множество A’= {4, 8, 12, 16, 20, 24, 28, …}, что совпадает со множеством B.

Иначе говоря, мы сопоставили каждому элементу a множества A элемент b из множества B посредством следующего правила сопоставления b = 4a, следовательно, количество эле- ментов в множествах совпадает. Таким образом, утверждение, что чисел, кратных 4, столько же, сколько и всего целых чисел, можно считать доказанным. Хотя наша интуиция утверждала, что их как минимум в 4 раза меньше.
РАВНЫЕ ОТРЕЗКИ
Рассмотрим пример из геометрии. Пусть имеется два отрезка A и B разной длины. Если провести через концы этих отрезков прямые, они пересекутся в точке C. Теперь обратите внимание, что можно про- вести отрезок от С к любой точке отрезка B, при этом он будет проходить через точку на А и свяжет точку на А с точкой на B единственным образом. Фактически, мы каждой точке А привели в соответствие точку B. Следовательно, количество точек в отрезке А равно количеству точек в отрезке B, что опять противоречит нашей интуиции и глазам, ведь A явно короче, чем B. В чём же подвох?
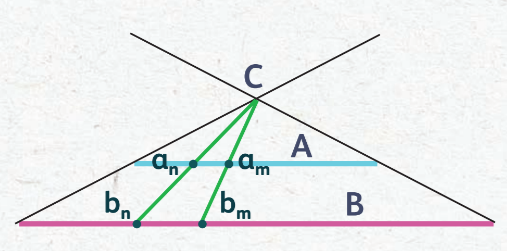
Начнём с определения понятия точки. В геометрии точка определяется аксиомами, которым она должна удовлетворять. В частности, геометрические точки не имеют длины, площади или объёма. Сколько точек можно уместить на отрезке, если длина и ширина точки равна 0? Сколько угодно, или, выражаясь языком математики, бесконечно много, ведь 0 + 0 + 0 + … + 0 = 0. Обратите внимание, что, складывая точки, вы не получите длину отрезка (!). Длина отрезка определяется иначе — через расстояние между точками. То есть любой отрезок состоит из бесконечного множества точек, в нашем случае A = {a1, a2, a3, …} и B= {b1, b2, b3, … }. Элементы (точки) этих множеств (отрезков) мы соотнесли через прямую, проходящую через точку C, следующим образом: c→a1→b1, c→a2→b2, c→a3→b3… Следовательно, совпадают мощности этих множеств, но не длины.
РАЗНЫЕ МОЩНОСТИ
Вернёмся к числовым множествам, а именно к рациональным числам. Это такие числа, которые можно представить в виде дроби n/m, где n, m ∈ N — принадлежат множеству целых чисел. То есть все эти числа представимы в виде какой-либо дроби, даже целые числа: у них в знаменателе стоит 1, например, 5/1 = 5. Мощности рациональных и натуральных чисел равны. Докажем это:

Все ли числа можно представить в виде дроби? Нет, не все. Например, √2 или π нельзя выразить дробью. Такие числа назы- вают вещественными. Изначально они были логическим обобще- нием рациональных, но у них впервые было обнаружено свойство несчётности, то есть оказалось, что их невозможно пронуме- ровать! Покажем это на интервале (0, 1). Пусть все-все числа x1, x2, x3,…из этого промежутка представлены в следующем виде:
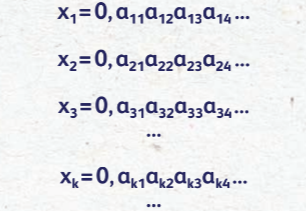
и так далее (их будет бесконечно много). Здесь aij— некоторые натуральные числа. Далее предположим, что каждому такому xi возможно присвоить некое натуральное число i. Но обратим внимание на вот такое число: x = 0, d1, d2, d3, d4, …
где di ≠ aii или di ≠ 0 или di ≠ 1.Совпадает ли оно с каким-либо из ранее описанных чисел? Нет, потому что оно всегда отличается хотя бы на одно значение (di ≠ aii). То есть число x оказалось не- учтённым, иначе говоря, ему не досталось номера. Так мы пришли к противоречию: как бы числа рассматриваемого промежутка ни были пронумерованы, всё равно найдётся число из этого же промежутка, которому не присвоен номер, следовательно, мощность множества вещественных чисел больше.
Таким образом, мы приходим к выводу, что существуют множества более мощные, чем бесконечные счётные множества. В частности, вещественные числа, мощность которых принято называть континуум. Знание основ теории множеств — залог понимания многих разделов математики. Но порой выводы, к которым она нас подводит, могут сильно разниться с нашей интуицией и жизненным опытом. Мы затронули лишь некоторые свойства множеств, но, надеемся, смогли показать безумное великолепие этой теории.
Заглавное изображение: Unsplash






