Сто орехов — это куча? Конечно! А два? Ну нет. Как тогда насчёт шести? И где же граница кучи? Сколько на голове должно быть волос, чтобы человек не считался лысым?
РОЖДЕНИЕ ПАРАДОКСА
Подобные вопросы интересовали в детстве, наверное, каждого: где куча, а где не куча? Эту же ситуацию обсуждали попугай, слонёнок, удав и мартышка в книге Григория Остера: сколько орехов нужно набрать, чтобы получилась куча? Попугай решил проблему быстро: много орехов! Правда, на вопрос слонёнка «А много — это сколько?» после паузы последовал неубедительный ответ «много — это много». После этого выяснилось, что 10, и даже 9 орехов — это явно куча, 2 и 3 — нет, а вот на шести попугай оказался в тупике.
Собственно, парадокс-то в том и состоит, что если мы берём «не кучу» орехов и последовательно добавляем по одному ореху, то в какой-то момент «не куча» должна стать «кучей». И всё благодаря всего одному ореху?
Этот парадокс первым сформулировал Евбулид из Милета, живший почти 2500 лет назад. Только он говорил не об орехах, а о зёрнышках. Согласитесь, так даже эффектнее: одно зерно — не куча, миллион — точно куча, значит, если добавлять по одному, то в какой-то момент «не куча» станет кучей! От одного зёрнышка!
Вариантов у этого парадокса множество. Допустим, у человека начинают выпадать волосы с головы — по одному. В какой момент можно сказать, что он лысеет? Или вот другой пример. Если в комнате 0 °C, там тепло? Нет. А 25? Конечно. Будем прибавлять по градусу (для пущей эффектности можно и по одной десятой градуса). Когда же станет тепло?
В ЧЁМ ПОДВОХ?
Парадокс основан на нашем интуитивном представлении, что одно зёрнышко не образует кучи (это очевидно) и добавление его к совокупности таких же зёрнышек не влияет на превращение этой совокупности в кучу. Но в действительности мы сталкиваемся с противоречием — куча из зёрен существует. Проблема кроется в определении понятия «быть кучей». В этом парадоксе мы пытаемся понять, принадлежит ли данный объект (например 6 орехов) некоему множеству объектов (куче орехов). В математике задачи такого типа встречаются на каждом шагу: например, требуется доказать, что четырёхугольник является параллелограммом или что функция является монотонной. Как мы решаем такие задачи?
Прежде всего, у нас есть чёткое определение параллелограмма, и мы пытаемся доказать, что для нашего четырёхугольника выполняются все условия (стороны попарно параллельны). Но самое главное — есть конкретное определение. В случае же с терминами «куча», «лысина», «тепло» точного определения нет. Если бы мы определили, например, кучу орехов как «множество, содержащее не менее 7 орехов», то мы бы точно знали, что 6 орехов — не куча, а 7 — куча. Но на деле такого определения нет, и более того, понятие «куча» может быть у каждого своим, в отличие от определения параллелограмма. Да и если бы определение было, оно вряд ли является разумным: действительно, получается, что 7 — куча, а 6 — уже нет?
ВЕРОЯТНОСТНЫЙ ПОДХОД
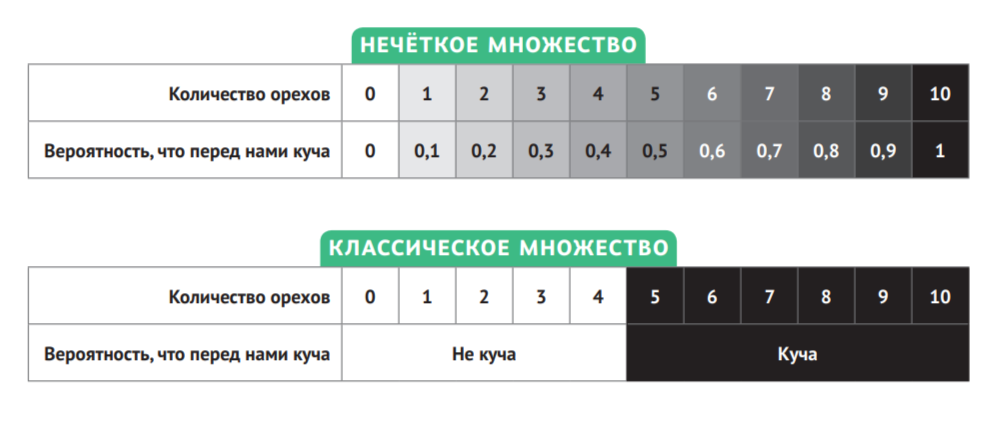
На самом деле решение может быть таким. Давайте называть объект кучей или не кучей с некоторой вероятностью. Например, 0 орехов — не куча, то есть куча с нулевой вероятностью. 10 орехов — точно куча, то есть куча с вероятностью 1. А все промежуточные значения определим так: если число x от 1 до 9, то множество из x орехов будем считать кучей с вероятностью x / 10. Иначе говоря, 6 орехов — на 60 % куча, а 7 — на 70 %. Таким образом, добавление ореха не делает из «не кучи» кучу, но добавляет вероятность того, что получилась куча.
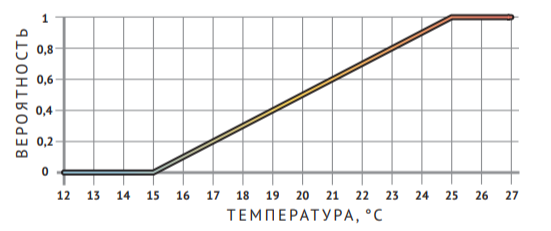
В случае с температурой в комнате можно поступить аналогично. 5 °C — точно не тепло, 25 °C — точно тепло, а дальше добавление 1 градуса к 5 дает прибавку в 0,05 к вероятности тепла. Так, 15 °C — тепло с вероятностью 0,5; а 20 °C — тепло с вероятностью 0,75. И конечно, мы можем задать все параметры иным образом. Например, будем считать, что 15 °C — тепло с вероятностью 0; 25 °C — тепло с вероятностью 1, а один градус добавляет по 0,1 к вероятности. Тогда «тепло с вероятностью 0,5» будет, когда температура составит 20 °C, а не 15, как в прошлом примере. Конечно, результат зависит от определения, но согласитесь, разница с определением «если больше 20 °C, то тепло, иначе — нет» есть — и существенная: исчезает резкий переход от «не тепло» к «тепло». Эту идею можно наглядно изобразить на графике. Отложим по горизонтали градусы, а по вертикали — вероятность «тепла» со значениями от 0 до 1: 0 — совсем не тепло, а 1 — точно тепло. Тогда наш последний пример может быть изображён так:
Похожим образом можно разобрать и следующий пример. Допустим, мы попытаемся проанализировать, насколько страшно вам прыгать с некоторой высоты. С высоты 0 см — точно не страшно. С высоты 400 см прыгать страшно всем (каскадёров в расчёт не берём). Но где граница? Опять же, если не вводить вероятности, то сложно поверить в тот факт, что до какого-то момента было не страшно, а потом прибавился один миллиметр — и стало страшно. Соответственно, поступаем так же, как в прошлый раз: будем считать, например, что каждые четыре сантиметра добавляют 0,01 к вероятности того, что страшно. В этом случае сорокасантиметровая высота — «страшно на 0,1»; двухметровая — «страшно на 0,5», а трёх метровая — «страшно на 0,75». Разумеется, если подобные вероятности кажутся вам не слишком разумными (например, вы считаете, что и 2 метра —однозначно страшно), вы можете поменять значения вероятности так, как вам нравится. Главное — идея, что всё происходит не одним скачком, а постепенно с ростом вероятности.
НЕЧЁТКОЕ МНОЖЕСТВО И НЕЧЁТКАЯ ЛОГИКА
Если подойти к вопросу формально, то куча, о которой мы говорим, называется нечётким множеством (fuzzy set). Это понятие было введено в 1965 году американским математиком азербайджанского происхождения Л З как расширенное представление классического множества.
С этой точки зрения задача об орехах и куче решается просто. Каждому элементу может быть присвоено значение не только 0 или 1, но и любое от 0 до 1! То есть если мы видим шесть орехов, то оценка этого множества с точки зрения нечёткой логики может быть, например 0,6.
УПРАВЛЕНИЕ ТРАНСПОРТОМ И РАБОТА СТИРАЛЬНОЙ МАШИНЫ — ТОЖЕ НЕЧЁТКИЕ!
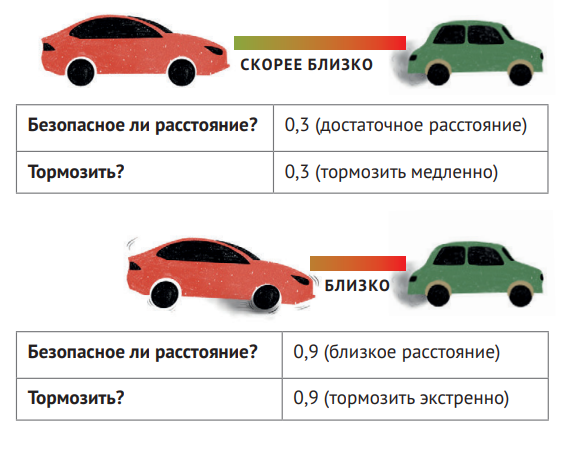
Одна из главных задач автомобилей с системой автопилота — удерживать безопасную дистанцию до другой машины. Для решения прекрасно подходит аппарат нечёткой логики.

Вряд ли бы вам понравилось ехать с таким автопилотом. Потому что ваша поездка состояла бы из череды резких торможений и ускорений. А если таких автомобилей будет несколько и они будут следовать друг за другом? Это не только опасно, но и крайне неэкологично — как известно, именно на ускорение расходуется большая часть топлива.
А вот и другой пример. Вы когда-нибудь задумывались, как работает стиральная машина? Действительно, даже если не обращать внимание на такие важные параметры, как тип ткани или количество белья, то очевидно, что длительность стирки должна напрямую зависеть от степени загрязненности белья и типа этой грязи. То есть если белье очень грязное, то машина должна стирать явно дольше, чем когда бельё почти чистое. Аналогично, сильно въевшуюся грязь надо отстирывать дольше чем свежие пятна. Но как это всё перевести в числа? И снова здравствуй, нечеткая логика! Теперь, если мы можем вероятностно определить тип грязи (например, жирная, средняя, не жирная), а также степень загрязнения (сильная, средняя, слабая), то мы можем, задав соответствующее правило, получить искомое время работы стиральной машины! Обратите внимание, что было бы весьма проблематично отделить сильное загрязнение от среднего, а вот вероятностный подход дает плавный переход, то есть равномерное изменение длительности стирки.
Что ж, хочется надеяться, что кучи стали для вас чуть менее парадоксальными, а нечеткие множества и нечёткая логика будут не раз выручать вас там, где классическая логика не справляется!
Заглавное изображение: Unsplash






