В повседневной жизни мы редко слышим загадочное слово – фрактал, но сталкиваемся с ним ежедневно. Деревья, горы, дым, растения и даже кровеносная система имеют фрактальную структуру. Применяют фракталы в разных областях: от алгоритмов сжатия изображения и до исследований сосудов живых организмов.

Так что же такое фрактал?

На языке математики фрактал — это множество со свойством самоподобия. Иначе говоря, каждый член множества является точной или приближённой копией части себя самого. Один из простых примеров, на котором можно понять, что такое фрактал — снежинка Коха. Давайте для начала её построим:

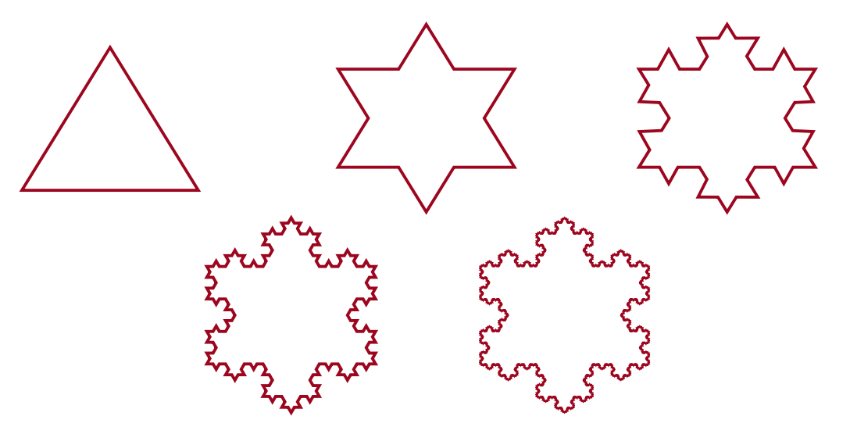
1. Начертим равносторонний треугольник.
2. На каждой стороне треугольника построим ещё равносторонние треугольники.
3. На каждой стороне меньших треугольников нужно построить ещё треугольники и так далее.

Снежинки Коха занимает ограниченную площадь, например, её можно ограничить окружностью определённой длины. Но при это снежинка имеет бесконечный периметр (!). Пусть изначально сторона треугольника равна единице, тогда на каждом шаге её длина увеличивается в 4/3 раза. Легко вывести соотношение длины стороны:

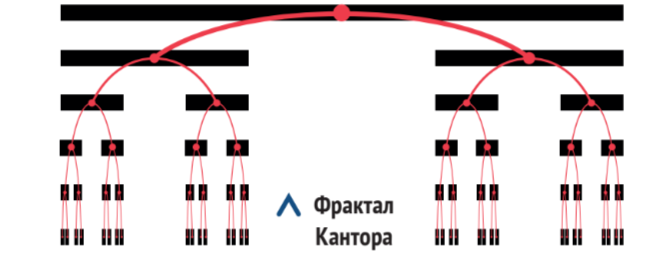
Снежинка Коха — геометрический фрактал. К ним также относятся множество Кантора, треугольник Серпинского, кривая Пеано и многие другие. Именно с них в XIX веке началась теория фракталов, так как в геометрических фракталах свойства само-подобия наиболее наглядны.

Фрактал описывается простыми правилами, которые необходимо выполнять многократно. На роль исполнителя этих действий прекрасно подходит компьютер, с появлением которого и связывают второе рождение фракталов. Фракталы — абстрактное математическое понятие, но самое удивительное, что в природе часто встречаются объекты, обладающие его главным свойством — самоподобием. С этим связано два основных направления практического применения теории фракталов. Во-первых, это попытка копировать природный фрактальный объект, используя упрощённую математическую модель. В этом направлении больших результатов достигла компьютерная анимация. Во-вторых, анализировать природный объект и выявлять в нем фрактальные структуры.

Фракталы в природе

Фрактальные свойства имеют кораллы, морские звёзды и ежи, брокколи, береговые линии и горные хребты, снежинки. Один из наглядных примеров фрактальной структуры — дерево. От ствола дерева отходит множество веток, а от них — ветки по- меньше и так далее. Дерево обладает главным свойством фрак- тала — самоподобием: каждая ветка подобна всему дереву.

Правило Леонардо о ветвях

В XlV веке Леонардо да Винчи вывел правило о толщине ветвей деревьев: «общая толщина ветвей на определённой высоте всегда равна толщине ствола». Учёные не нашли точного объяснения данному феномену: одни связывают это с транспортировкой воды в коре дерева, другие — с устойчивостью дерева к внешним механическим воздействиям. Похожим образом устроена и кровеносная система человека: от артерий отходят более тонкие сосуды — артериолы, а от них — самые мелкие сосуды — капилляры. Опираясь на фрактальные свойства кровеносных сосудов, учёные изучают и объясняют различные аномалии в организме человека.

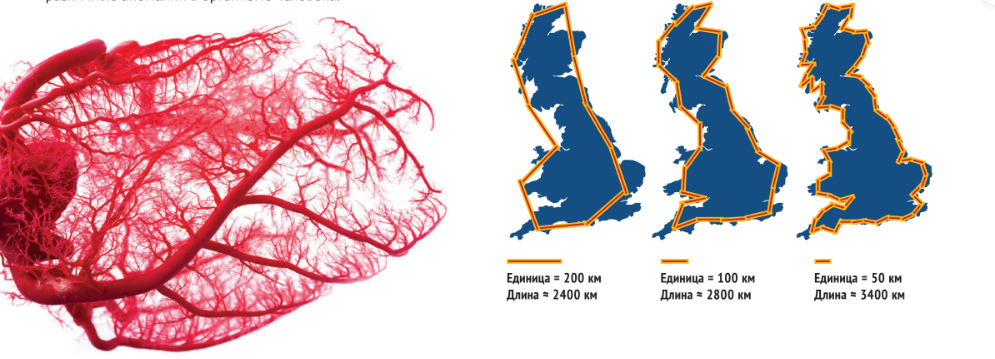
Парадокс береговой линии

Береговая линия — самый необычный пример фракталов. Если всё остальное человек может увидеть целиком, то с береговой линией намного сложнее: стоя на земле, можно наблюдать лишь небольшой участок берега.

Парадокс береговой линии Из-за фрактальных свойств береговой линии невозможно точно измерить её длину. Изгибы береговой линии имеют разную длину, от нескольких километров до тысяч километров, поэтому невозможно подобрать наименьший отрезок, с помощью которого будет проводиться измерение. Так, если разделить береговую линию на отрезки по 50 км и посчитать суммарную длину отрезков, она будет сильно отличаться от длины, полученной при суммировании отрезков в 100 км.

С этим парадоксом столкнулся в 1951 году английский математик Льюис Фрай Ричардсон, он заметил, что Португалия определила свою сухопутную границу с Испанией в 987 км, тогда как Испания, в свою очередь,— в 1214 км. Разрешили эту проблему так: единицу измерения стали принимать за минимальный отрезок. Например, если длина береговой линии измеряется в километрах, то небольшие изгибы, длина которых намного меньше одного километра, не учитываются.

Где применять теорию фракталов?

Фрактальный алгоритм компрессии изображения имеет высокий коэффициент сжатия: изображение становится гораздо меньше по размеру, что экономит память компьютера. Коэффициент сжатия при использовании фрактального алгоритма примерно сопоставим с самым популярным методом сжатия JPEG. Суть метода в обнаружении самоподобных участков в изображении, что позволяет при после- дующем увеличении сжатого изображения сохранить качество изображения.

В искусстве

Облака, деревья, цветы, горы, море и многие другие природные объекты, которые можно увидеть в компьютерных играх и мультфильмах, сгенерированы с помощью фрактальных алгоритмов. При использовании фрактального метода не нужно отдельно прорисовывать каждую деталь графического объекта (ветвь дерева, верхушку горы или лепесток цветка): достаточно лишь задать начальные параметры алгоритму, а всю оставшуюся работу сделает компьютер. Благодаря этому можно также достаточно легко и быстро видоизменять объект, поменяв лишь начальные параметры алгоритма.

В борьбе с раком

Современное медицинское оборудование (МРТ и томография) позволяет получить огромный объём цифровых данных о внутренних органах пациента. Компьютер проводит математический анализ этих данных и выявляет фрактальные структуры. Так, раковые опухоли и эмфиземы имеют более сложную структуру, а здоровые участки более простую. Принцип самоподобия фрактала позволяет выявить отклонения на самых ранних стадиях и делать это автоматически, без участия врача. Модель фрактального анализа при диагностике рака лёгких. Раковые опухоли — аномальный, быстрый рост клеток, который сопровождается образованием новых беспорядочных кровеносных сосудов. При том, что здоровые сосуды имеют упорядоченную фрактальную структуру.

В строительстве

Современные инженеры используют высокопрочные кабеля, кото- рые сплетены по фрактальному принципу: кабель образован из пуч- ка меньших проводов, которые созданы из более мелких пучков и т. д. Мост Золотые ворота (Сан-Франциско, США) — один из при- меров применения подобной технологии.