Число, равное отношению длины окружности к диаметру, принято обозначать греческой буквой π. Пожалуй, это самая популярная «математическая буква». Ведь её используют архитекторы, физики, астрономы, химики, биологи и многие другие специалисты.

Великое соревнование

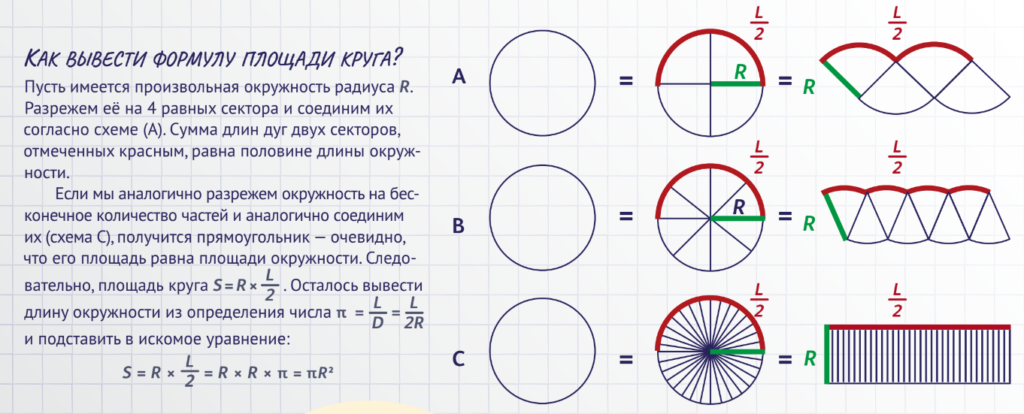
Если измерить верёвкой длину окружности, получится, что она равна приблизительно трём её диаметрам. Человечество выяснило это ещё в древности. Удивительно то, что данное соотношение верно для любой окружности, какой бы размер она ни имела: от пуговицы до колеса. Иначе говоря, все окружности связывает некая константа, причём точно известно, что она чуть больше трёх. Многие столетия она не давала покоя мыслителям, поскольку очевидно имела большое значение и была почти высчитана. Но это «почти» растянулось на тысячелетия. В Древнем Вавилоне π полагали равным 3. Это следует из формулы площади круга S = P:12 (где l — длина окружности), найденной в расчётах вавилонян. Это очень грубое приближение.

Число, равное отношению длины окружности к диаметру, принято обозначать греческой буквой π. Пожалуй, это самая популярная «математическая буква». Ведь её используют архитекторы, физики, астрономы, химики, биологи и многие другие специалисты. 232, 8 м 146, 6 м которое даёт большую погрешность в вычислениях. В Вавилоне, конечно, обозначение π не использовали — мы подразумеваем под этой буквой отношение длины окружности к её диаметру. Древние египтяне подошли к делу серьёзнее. В известном документе «Папирус Ринда» (XX–XVII века до н. э.) описаны решения многих прикладных математических задач.

Также в нём сформулировано правило для вычисления площади круга: S =(8:9*d)²(где d — диаметр окружности), откуда следует, что π равно 3,16049… Как эта формула была выведена, точно неизвестно. Скорее всего, египтяне стремились свести поиск площади круга к поиску площади квадрата: круг диаметром 9 очень близок по площади к квадрату со стороной 8.

Более точное значение числа π было получено в Древней Греции при решении классической математической задачи о квадратуре круга. Используя циркуль и линейку, нужно было построить квадрат, равный по площади данному кругу. Алгебраически это можно записать так: a² = πR², где а — сторона квадрата, R — радиус круга. Следовательно, a=R√π, то есть задача сводится к построению от- резка длины √π. Но всё же Архимед нашёл достаточно точное приближение числа π ≈ ≈ ≈ 3,142857. Более того, он указал границы промежутка, которому принадлежит π: «Периметр всякого круга равен утроенному диаметру с избытком, который меньше одной седьмой части диаметра, но больше десяти семьдесят первых». В работе «Изме- рение круга» Архимед доказывает цепочку неравенств: 3 < π < 3 . Прийти к тако- му выводу учёному помогли вписанные и описанные многоугольники.

Неразрешимость задачи о квадратуре круга

Почему греков так волновала квадратура круга? Дело в парадоксе этой задачи. С точки зрения греческих математиков, если фигура имела площадь, то существовал равновеликий ей квадрат. Круг очевидно имел площадь, но построить равновеликий квадрат никак не получалось. Методами высшей математики было доказано, что решить эту задачу в исходной формулировке невозможно. Иррациональность π была доказана Иоганом Ламбертом в 1766 году в труде «Предварительные сведения для ищущих квадратуру и спрямление круга». А полное доказательство неразрешимости задачи о квадратуре круга при по- мощи циркуля и линейки представил в 1882 году Фердинанд фон Линдеман, доказав трансцендентность этого числа. Иными словами, оно не может быть корнем многочлена с рациональными коэффициентами.

В 1990-х американский студент Колин Персивал запустил глобальный проект PiHex. Любой житель Земли, имевший доступ в интернет, мог стать участником коллективных вычислений отдельных цифр двоичной записи числа π. В проекте приняли участие 1885 компьютеров, которые потратили на расчёты 1,3 миллиона процессоро-часов. Вычисления на каждой отдельной машине велись в фоновом режиме. Таким образом, к 11 сентября 2000 года — дате окончания проекта — участники получили цифру, стоящую на 40 000 000 000 000-м месте двоичного числа π. Это оказался ноль.

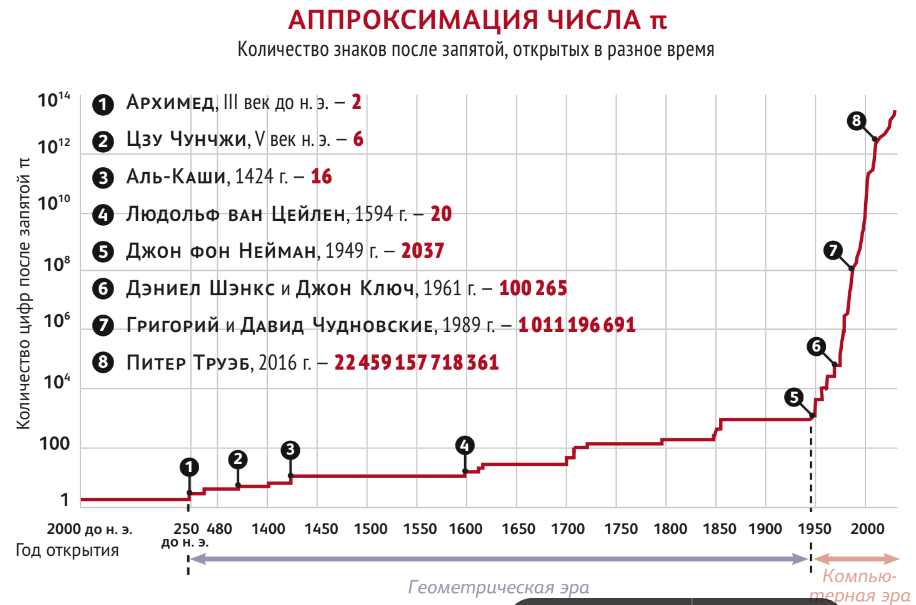
Математики открывали всё новые и новые знаки после запятой. Эти результаты носили скорее спортивный характер. Так, например, для большинства космологических расчётов достаточно 39 цифр. Это значит, что для вычисления окружностей, сопоставимых с наблюдаемой Вселенной, погрешность будет в пределах одного атома. Но такие задачи-тренажёры оказали большое влияние на развитие математических методов. Например, Архимедов подход заложил основы интегрального исчисления, а компьютерные расчёты открыли нам алгоритмы сверхбыстрого умножения. Вдобавок это отличный способ проверить быстродействие и эффективность суперкомпьютеров.

Число π вокруг нас

Представьте себе верёвку длиной 40 075 км — её хватит, чтобы опоясать Землю вдоль экватора. Теперь добавим к ней ещё 1 метр и снова обернём Землю. Сможет ли в образовавшийся зазор пролезть кошка? Прежде чем мы начнём решать эту задачу, обратите внимание на первую мысль, которая пришла вам в голову: что такое 1 метр в сравнении с 40 075 км?! Вспомним формулу расчёта длины окружности: l=2πR. Ширина зазора будет равна разности радиусов двух окружностей:

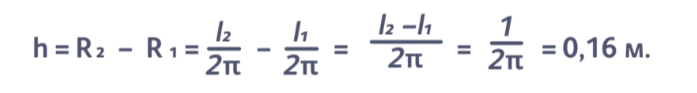
Итак, за кошку можно не волноваться: она сможет проползти под верёвкой! Как видно из расчётов, радиус окружности не играет здесь никакой роли, и неважно, планета это или атом водорода. Когда речь идёт об окружностях, присутствие числа π не удивляет. Но π появляется и там, где, казалось бы, никаких окружностей нет. В 1777 году французский математик Жорж-Луи Леклерк де Бюффон решал следующую задачу: «Предположим, пол сделан из чередующихся паркетин двух цветов. Какова вероятность, что брошенная иголка упадёт так, что пересечёт линию стыка паркетин?» Кидая иголки по одной и записывая на каждом шаге отношение иголок, пересекающих линию стыка, к количеству брошенных, учёный получал всё более точное приближение искомой вероятности. При увеличении количества бросков до 10 000 значение вероятности приблизилось к некоторой величине, равной примерно 0,6366. Поделив двойку на это число, мы получим 3,14169, что близко к значению π. Это действие вытекает из аналитического решения задачи, которое мы не будем приводить. В итоге получается следующая формула:

Напомним, что вероятность p мы можем оценивать как отношение иголок, пересекающих стык, к общему их количеству. И чем больше бросков мы сделаем, тем точнее будет определена эта вероятность, а следовательно, и число π. Вот так, просто бросая иголки на пол, можно найти π!

Фундаментальность числа π математики объясняют тем, что через него выражаются соотношения между дуговыми и линейными размерами объекта. Причём это соотношение одинаково для объектов во всех уголках Вселенной. Если утверждение верно, из него вытекает одинаковость свойств пространства, равно как и сохранение его физических свойств — изотропность. На этом основан один из главных законов физики — закон сохранения момента импульса.