По статистике, большинство людей предпочитает простые задачи сложным. Мы охотно берёмся решать то, что нам очевидно по силам. Похожим образом обстоит дело с ответами на вопрос: «Почему вы любите математику?» Подавляющее большинство отвечает: «Потому что у меня хорошо получается». А что делать, если не получается?
Каждый оказывался в ситуации, когда не совсем понятно, как подступиться к задаче. Первое, что вы делаете, — внимательно перечитываете её условие. Но алгоритм действий всё равно не складывается. Время идёт, а вы всё глядите в условие и не понимаете, с чего начать. Но раз решить не удаётся, не лучше ли бросить задачку и делать то, что получается? Нет. Это всё равно что, занимаясь альпинизмом, научиться забираться на холм высотой 10 мет ров, а когда дело дойдёт до первого непростого восхождения, плюнуть и всю оставшуюся жизнь подниматься только на 10-метровые холмы. И вся красота гор, вся радость преодоления пройдёт мимо! Так же с математикой. Сейчас мы рас- смотрим несколько приёмов, которые помогают не сдаться и найти направление, в котором можно начать думать, чтобы решить-таки задачу.
Будьте внимательны
Начинать всегда надо с внимательного чтения условия. Есть такая задачка: Васе 10 лет, а Маше через 3 года будет на 2 года больше, чем было бы через 5 лет Васе, будь он на 2 года старше. Сколько сейчас лет Васе? Многие долго и упорно прорубаются через эту задачу, хотя ответ, конечно, «10» — спрашивают, как ни парадоксально, возраст Васи, который указан в первой же фразе! Жульничество? Никак нет, просто задачи бывают разные, а отвечать надо исключительно на поставленный вопрос.
А вот ещё задача, советую попробовать решить её устно: попросите кого-ни- будь медленно читать условие, а сами считайте. Главное — не сбейтесь! В автобусе было 10 пассажиров. На первой остановке вошло ещё пятеро, трое вышло. На второй вошло семеро, а вышло пятеро. Дальше вошло двое, вышло четверо. Потом вошло четверо и столько же вышло. Потом вошло трое, а вышел один. Наконец, вошёл один, а вышло пятеро. Сколько всего было остановок? Ну как, попались? Уверен, многие сейчас считали пассажиров, а не оста- новки. Конечно, этого не случилось бы, если б задача была перед глазами, но опять-таки не все внимательно читают условие. А ведь в ряде случаев это ключ к решению проблемы.
Начните с малого
Допустим, условие хорошо прочитано и понято. Что дальше? Первый совет можно сформулировать так: сделайте хоть что-нибудь. Есть такой анекдот: некто усердно молится Богу, чтобы тот послал ему выигрыш в лотерее. День молится, два, месяц, год… В конце концов ангелы не выдерживают, летят к Богу: мол, дай ты ему уже выиграть, он так просит! А Бог отвечает: «Я бы рад, но пусть он хотя бы лотерейный билет купит». М раль проста: если сидеть и просто смотреть на задачу, ничего не выйдет. Нужно сделать хоть что-нибудь. Посмотрим, как это работает.
Пример 1
Можно ли расставить по кругу различные числа так, чтобы каждое из них было равно сумме соседних? Попробуем «сделать хоть что-нибудь». Начнём подбор со случайных чисел и по- стараемся сформировать искомый круг. Понятно, что с нуля начинать плохо: тогда второе число будет равно сумме соседей только в том случае, если третье будет равно второму, а нам нужны разные числа.
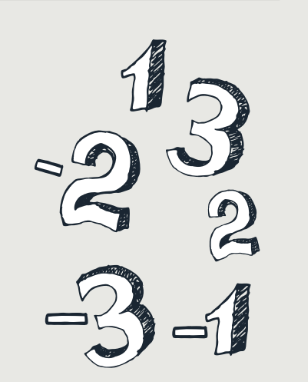
Допустим, первое число — 1. Если второе — 2, то третье равно 1 (так как второе должно быть равно сумме первого и третьего), а это повторение, плохо. Ладно, пусть второе число равно 3. Пока имеем «1, 3». Третье число должно равняться 2, чтобы 3 было суммой своих соседей. Итак, «1, 3, 2». Аналогичным образом получаем, что четвёртое равно –1, пятое –3, а шестое –2. Осталось увидеть, что круг замкнулся, ведь –2 как раз равно сумме –3 и 1! Таким образом, искомые шесть чисел по кругу это 1, 3, 2, –1, –3, –2. Разумеется, это не единственный пример, но нас и не просили привести все. Мы показали, что это возможно.
Что же помогло нам решить задачу? А то, что мы с чего-то начали — просто подбирали числа. Допустим, первое число — 1. Если второе — 2, то третье равно 1 (так как второе должно быть равно сумме первого и третьего), а это повторение, плохо. Ладно, пусть второе число равно 3. Пока имеем «1, 3». Третье число должно равняться 2, чтобы 3 было суммой своих соседей. Итак, «1, 3, 2». Аналогичным образом получаем, что четвёртое равно –1, пятое –3, а шестое –2. Осталось увидеть, что круг замкнулся, ведь –2 как раз равно сумме –3 и 1! Таким образом, искомые шесть чисел по кругу это 1, 3, 2, –1, –3, –2. Разумеется, это не единственный пример, но нас и не просили привести все. Мы показали, что это возможно. Что же помогло нам решить задачу? А то, что мы с чего-то начали — просто подбирали числа.
Детализируйте условие
Иногда очень полезно задать себе уточняющий вопрос. В одном эксперименте 600 участникам предложили решить задачу: Даны четыре точки, расположенные как вершины квадрата. Требуется провести карандашом три отрезка, чтобы зачеркнуть все точки и чтобы карандаш, не отрываясь от бумаги, вернулся в исходную точку. Справились с задачей единицы. А затем участникам задали вопрос: какая фигура получится в итоге? Догадавшись, что треугольник, почти все решили задачу.
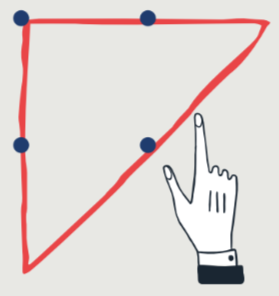
Спрашивается, что мешало задать этот вопрос самим себе? Ничего, но это очень важно — задавать себе правильные вопросы, которые помогут разобраться в конструкции задачи.
Пример 2
Арбуз разрезали на 4 части и съели. В результате получилось 5 корок. Как такое возможно? Что удивляет в этой задаче? Пожалуй, то, что корок больше, чем частей. Действительно, обычно съедаешь мякоть одного куска — остаётся одна корка. А здесь не так. Зададим себе вопрос: в каком слу- чае корок может оказаться больше, чем кусков? Иначе говоря, каким должен быть кусок, который даёт две корки? А это уже понятно: он должен состоять из мякоти, соединяющей две корки, — такой кусок легко получить, если сделать в арбузе цилиндрический разрез. Оставшийся арбуз режем продольно на 3 части и получаем 5 корок из 4 кусков. Вуаля!
Создавайте варианты
Ещё одна полезная идея. Наверняка многие из вас играли в игру «Сделай из козы волка». Суть её в том, чтобы образовать из одного слова другое, меняя по од- ной букве так, чтобы каждый раз получались осмысленные слова. Например, из слова «рог» сделать «май» можно так: рог — рой — рай — май. Игра несложная, но иногда можно застопориться надолго, в частности, сделать из «мухи» «слона» могут немногие. Но мы с вами рассмотрим пример из названия. Как превратить «козу» в «волка»? Возможно, кто-то с ходу написал цепочку — молодцы! Это как если бы вас озарило при решении задачи — круто, что тут скажешь. Но вдруг не озарило? Что делать: сдаться? Не спешите. Попробуем поступить так. У нас есть «коза». Какие слова можно получить за один ход?
Накидайте варианты на листочке, а потом посмотрите наши: роза, поза, доза, лоза, кора, кома, кода, кола (орешек есть такой, а не только напиток), коса. Пока этого хватит. Идём дальше — нам надо получить «волк», то есть образовать цепочку коза… — волк.
Первый шаг мы сделали, получили много вариантов. А как насчёт последнего? Из каких слов можно получить «волк»? Полк, толк, воля. А теперь попытаемся связать слова из первой и второй групп. Для этого поищем похожие слова — такие, в которых одинаковые буквы стоят на тех же местах. Например, поза и полк. Можно ли получить из одного другое?
Конечно: поза — пола (пиджака, например) — полк. Вот мы и получили нужную цепочку: коза — поза — пола — полк — волк . Примерно так же можно подходить к решению задач. В большинстве из них есть начальные данные и то, что нужно найти. В предыдущем примере в роли на- чальных данных выступала коза, а в роли искомого ответа — волк. Соответственно, иногда стоит рассматривать всевозможные первые шаги, а иногда — какие шаги могут привести к ответу. Проиллюстрируем эту идею примером.
Пример 3
На доске написано число 3. За ход разрешается умножить число на 2 либо поменять в нём цифры. Можно ли с помощью этих операций получить число 57?
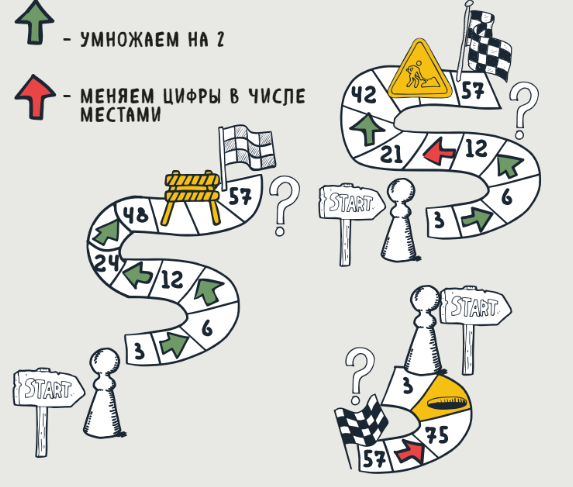
Если пойти с начала, то первые шаги очевидны: 3 — 6 — 12. Дальше начинает- ся ветвление: 24 или 21, затем 42 или 48, и так далее. Попробуем зайти с конца. Как могло образоваться 57? Очевидно, только из 75, ведь, умножив что-то на 2, мы по- лучили бы чётное число, а 57 — нечётное. Но по той же самой причине 75 нельзя получить никак иначе, кроме как пере- ставив цифры в числе 57. То есть 57 и 75 образуются только друг из друга, а так как исходное число у нас 3, значит, получить в конце 57 мы не сможем. Вот так анализ концовки помог нам решить весьма не- простую задачу. А вот ещё пример на «сближение» начала с концом.
Пример 4
В квадрат площадью 20 вписан круг. Найдите площадь этого круга. Задача несложная, но очень хорошо иллюстрирует идею. Что мы можем найти, зная площадь квадрата? Первое, что приходит в голову, — его сторону. Теперь попробуем с конца: как найти площадь круга?
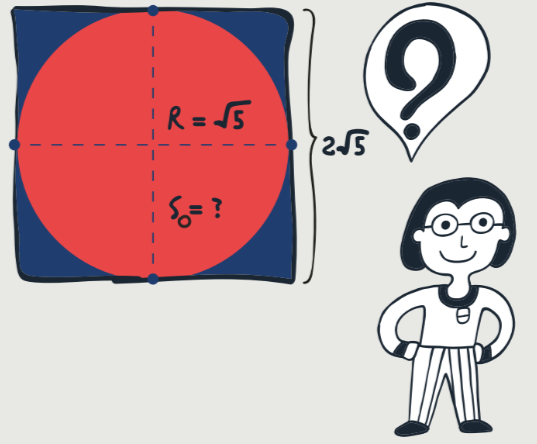
Конечно, через его радиус, по формуле S = π R 2 . Значит, задачу можно переформулировать: как, зная сторону квадрата, найти радиус вписанного в него круга? А это уже не задача — очевидно, нужно просто поделить сторону квадрата пополам. Осталось досчитать. Раз площадь квадрата равна 20, то его сторона — √20, то есть 2√5. Тогда радиус искомого круга равен √5 (он вдвое меньше), а значит, площадь круга составляет 5π. И напоследок хочется вспомнить старый советский мультфильм про удава, мартышку, попугая и слонёнка. Попугай учится летать, очень боится и спрашивает, что делать, если вдруг у него не получится. На это друзья хором отвечают ему: «По- пробуешь опять!» И этот совет отлично применим к «нерешаемым» задачам: не бойтесь искать и пробовать, а если не получается — попробуйте опять!
Заглавное изображение: Unsplash