Температура — что может быть проще? Высокая — значит, тепло или жарко, низкая — наоборот, холодно. А если нулевая? Оказывается, нулей несколько.
Фаренгейт взял за основу стабильное состояние смеси воды, льда, соли и нашатыря. Этот состав был популярен тогда у торговцев рыбой и мясом. Смесь достаточно долго поддерживала температуру около –18° (Цельсия), памятную Фаренгейту по чрезвычайно холодной зиме 1709 года. Полагая, что таких морозов больше не будет, он принял её за ноль для своей шкалы. Другой точкой стала температура тела здорового человека, которую многие учёные того времени полагали строго постоянной. Ей Фаренгейт присвоил значение 96° — такое странное значение было взято для удобства градуировки шкалы термометра.
«Домашняя» термодинамика
Какой бы ни была шкала, измерение температуры основано на двух фактах. Первый: холодные тела и вещества нагреваются от тёплых, и процесс этот происходит до тех пор, пока температуры не сравняются, то есть наступит тепловое равновесие. Если же захочется тело охладить, то естественным путём этого не сделать. Свидетельство тому — счета за электроэнергию, израсходованную холодильником, где охлаждение принудительное. Второй факт: тела и вещества, находясь в одном и том же агрегатном состоянии, при нагревании расширяются (увеличивают объём), а при охлаждении — сжимаются. Но это не касается воды: изменение её объёма — процесс нелинейный, и меньше всего места вода занимает не при замерзании, а при +4 °С. К счастью, при нормальных условиях многие вещества ведут себя вполне предсказуемо. Термометры, в которых при изменении температуры меняется объём рабочего тела (воздуха или жидкости), исправно несут службу со времён Л В.
Шкала Фаренгейта получила распространение в англоязычных странах, но к 60-м годам прошлого века была вытеснена более удобной и логичной шкалой Цельсия, опирающейся на свойства чистой воды. Градусы Фаренгейта применяются только в шести странах (одна из них — США). Вернёмся к рассказу Джека Лондона. Отметка +20° по Фаренгейту соответствует в привычных нам градусах Цельсия –6,7 °. Довольно холодно!
А все-таки они расширяются!
Первыми успеха в исследовании влияния температуры на объём веществ добились англичанин Д Д и француз Ж Л Г- Л. Произошло это в самом начале XIX века. Их экспериментальные установки во многом повторяли старинные флорентийские термометры времён Г: вверху находилась колба с газом, из которой вниз уходила трубка, опущенная в сосуд со ртутью. Жидкий металл, выдавливаемый атмосферным давлением, частично заполнял трубку, образуя нечто вроде поршня в цилиндре. Когда газ нагревался (колбу обливали кипятком), его давление повышалось, и он выдавливал ртуть в трубке. Изменение объёма газа легко посчитать, зная диаметр трубки и смещение уровня ртути.
Многие считают, что абсолютный нуль — это температура космического вакуума. Ведь температура —это мера средней кинетической энергии частиц среды, а если их нет, то и энергия равна нулю. Это не так: космическое пространство — вовсе не вакуум, а очень разрежённый газ с довольно высокой температурой, около 2,7К. Но его плотность настолько низка, что теплообменом можно пренебречь.
Логично предположить, что разные газы по-разному будут и расширяться. Дальтон экспериментировал с кислородом, азотом, водородом, углекислым газом. Но результаты опытов сильно озадачили — все газы вели себя одинаково. Этот факт Дальтон осторожно прокомментировал так: «В общем, я не вижу достаточной причины, мешающей нам заключить, что все “упругие” газы при одном и том же давлении одинаково расширяются при нагревании». Гей-Люссак подошёл к проблеме ещё обстоятельнее. Исследовав поведение разных газов, он заключил: «Все газы и все пары одинаково расширяются при одном и том же повышении температуры. Для газов увеличение объёма каждого из них в пределах от температуры таяния льда до температуры кипения воды равно 100/26666 первоначального объёма». Другими словами, учёный определил коэффициент теплового расширения (то есть относительное изменение объёма при изменении температуры на 1 °) — 0,003744 град−¹, одинаковый для любых газов, взятых при атмосферном давлении.
Можно сделать такой вывод: если при повышении температуры на 1 ° объём газа увеличивается на 1/267, то при охлаждении он должен иметь всё меньший и меньший объём, пока при –267 ° не обратится в ноль. Наступит момент, когда и температура, и объём газа станут нулевыми. Вот вам и абсолютный нуль!
Стремимся к идеалу На самом деле дела обстоят несколько иначе. Непреодолимая преграда — конденсация, превращение газа в жидкость. Но если держаться в стороне от экстремальных значений и придерживаться нормальных условий — температуры 0 °С и давления в 101 кПа, то газовые законы вполне могут предсказывать поведение реальных веществ. Стремление найти общий фактор привело к появлению модели идеального газа. Главная её черта — «замена» молекул и атомов абсолютно твёрдыми шариками, не взаимодействующими между собой. Собственный объём «шариков», их соударения и внутреннее строение во внимание не принимаются. Значение имеют только массы, скорости и удары о стенки сосуда, порождающие давление. Оказалось, что эта крайне упрощённая модель весьма неплохо объясняет газовые законы. И самое главное — раскрывает физическое содержание температуры.
Океан в капле
Модель идеального газа закономерно привела учёных к молекулярно-кинетической теории. Она исходит из простых положений: все тела состоят из частиц (молекул, атомов и ионов), все частицы непрерывно и хаотически движутся, время от времени упруго сталкиваясь. Казалось бы, что можно построить на таком примитивном фундаменте? Ни много ни мало, а связать макроскопические параметры газа: давление, объём и температуру — с микрохарактеристиками частиц (их массой и скоростью движения), попутно установив, что температура — вовсе не уровень чудесной «тепловой жидкости», а мера средней кинетической энергии атомов или молекул.
Привязка температуры к энергии — событие эпохальное, по значению не уступающее торжеству системы Коперника или теории электромагнетизма Максвелла. Особенно надо отметить австрийского физикатеоретика Л Б, основателя молекулярно-кинетической теории (МКТ) и статистической физики. Больц ман рассчитал, насколько прирастает энергия одной частицы идеального газа при изменении температуры на 1 °. Эта величина, равная 1,38 × 10−²³ Дж/К, теперь называется постоянной Больц мана. Оставался ещё один шаг. Способов напрямую измерять среднюю кинетическую энергию нет, поэтому определить температуру можно косвенным путём, через нагрев или охлаждение так называемых термометрических тел — воды, спирта, ртути, разрежённых газов, меняющих свой объём. Обилие таких веществ породило множество эмпирических шкал, градуируемых на основе экспериментов.
Почему он работает? На роль универсального термометрического тела лучше всего подходил… идеальный газ. Отчасти такая концепция уже получила воплощение в виде газового термометра, действие которого основано на законе Шарля, связывавшего температуру и давление. (Наиболее точным был водородный термометр.) Теоретическое обоснование предложил У Т, более известный нам как К. Нет, это не персонаж из «Звёздных войн» и не злодей из саги о Гарри Поттере. Томсон с полным правом занимает почётное место в ряду самых выдающихся учёных
мира: стать профессором теоретической физики в 22 (!) года — безусловное достижение! В 1848 году он предложил взять за основу модель идеальной тепловой машины, КПД которой зависит от разности температур нагревателя и холодильника, а также от количеств теплоты, поглощённых и отданных рабочим телом (любой газ, от водяного пара до продуктов сгорания топливных смесей). В качестве опорной точки берётся тройная точка воды (при давлении около 612 Па и температуре 0,01 °С вода может равновесно находиться одновременно во всех фазах — твёрдой, жидкой и газовой).
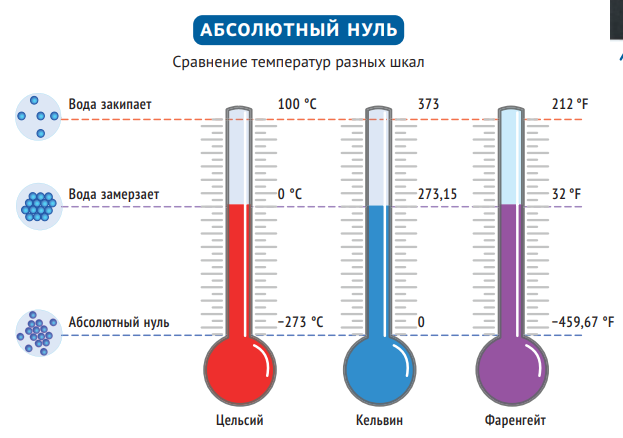
Температурная шкала Кельвина, ставшая одним из основных инструментов инженеров и учёных, легко соотносится с привычной шкалой Цельсия — к последней надо просто прибавить 273,15, и вы получите температуру в кельвинах, одной из семи основных единиц СИ.
От Цельсия к Кельвину K = °C + 273,15
От Кельвина к Цельсию °C = K − 273,15
Теоретически, отталкиваясь от неё, можно, измеряя поступление и отвод тепла, рассчитывать конечную температуру, названную термодинамической. На практике же оказалось, что определить точные количества теплоты как раз невозможно.
Проще взять уже известный коэффициент теплового расширения (его уточнённое значение равно 1/273,15), определить на его основе значение градуса и привязать к шкале точки замерзания и кипения чистой воды при нормальном атмосферном давлении. Получится привычная стоградусная шкала, которую нужно откалибровать по опорной точке. Представив теплообмен как средство изменения энергии молекул и атомов вещества, Томсон пришёл к идее минимально возможной температуры:при ней теплообмен становится невозможен, хаотическое (броуновское) движение частиц прекращается, а их средняя кинетическая энергия обращается в ноль. Более естественной точки отсчёта для температурной шкалы и быть не может!
От чего начинать?
Таким образом, термодинамическая шкала температур опирается на две опорные точки (абсолютный нуль и тройную точку воды, температура которой принята за 273,15 К), не зависит от рода вещества и принимается как фундаментальный параметр тепловых процессов. При этом абсолютный нуль недостижим в принципе.
Дело в том, что количество работы, необходимое для отвода тепла от вещества, существенно возрастает по мере охлаждения. Чтобы достичь нуля, потребуется бесконечное количество работы. Квантовая механика нам подсказывает, что атомы и молекулы даже при температурах, близких к абсолютному нулю, всё равно будут двигаться, пусть и минимально.
Сегодня удаётся получать температуры, отличающиеся от абсолютного нуля на миллиардные доли кельвина, пусть это и непросто. Казалось бы, и хватит, ведь предел недостижим в принципе! Но путешествие к нулю не прекращается: уж очень интересно ведёт себя вещество в таком первозданном холоде.
Как объясняет квантовая механика, по принципу неопределённости Гейзенберга нельзя одновременно точно определить и координату, и импульс объекта: произведение минимальных погрешностей их измерения есть константа. Следовательно, если атомы останавливаются, то их координаты можно определить точно, то есть погрешность обращается в нуль, но тогда неопределённость значения импульса стремится к бесконечности. Это значит, что их кинетическая энергия неограниченно растёт сама по себе, нарушая все законы сохранения, и никакого абсолютного холода не получается.






