Что есть число? Любая наука и теория строится на базовых понятиях, которые обычно интуитивно ясны и принимаются нами без доказательств (мы называем такие понятия аксиомами). Число в математике как раз и есть базовое понятие — это абстракция, используемая для количественного описания объектов. В зависимости от объекта изучения мы представляем числа так, как нам удобно.

Например, если взять число 4, в зависимости от решаемой нами задачи его можно представить как количество неких эле- ментов, например спичек, как отрезок длиной 4 см, как квадрат площадью 4 см2, как положение точки на числовой прямой или даже как произведение двух чисел. Также стоит помнить, что запись числа «четыре» как «4» — не более чем форма записи, модель. В троичной системе счисления это число записывается как «11,» римскими цифрами — как «IV» и так далее.

С натуральными числами всё просто, дроби тоже можно представить как вполне осязаемые объекты — части целого. Но есть числа, которые нельзя представить в виде дроби, — иррациональные числа.

Первое иррациональное число

Всё началось примерно 37 веков назад — с числа, которое мы теперь называем квадратный корень из двух и обозначаем как √2. С точки зрения алгебры это такое число, которое при возведении в квадрат даёт 2. Тут следует сделать отступление и рассказать о математике тех времён, а именно о том, что она опиралась в первую очередь на геометрические представления. Свойства чисел и теоремы доказывались геометрическими методами, а величины всегда имели геометрический смысл. Так, например, иррациональные числа появились в математике раньше отрицательных и нуля, которые не имеют под собой элементарной геометрической основы.

Как же это могло выглядеть? Очень просто, многие алгебраические операции можно представить через геометрию. Например, умножение двух чисел — площадь прямоугольника, длины сторон которого Рис. 1. Площадь внешнего квадрата равна 4, Рис. 2. Древняя вавилонская табличка площадь внутреннего — половине внешнего имеют длины, соответствующие данным числам; возведение числа в квадрат — на- хождение площади квадрата со стороной, равной данному числу. Именно благодаря задаче, связанной с площадью, возникла идея о существовании числа, ранее не изучавшегося математикой.

Рассмотрим простую с точки зрения геометрии задачу. Разобьём квадрат площадью 4 на четыре единичных квадрата и проведём в каждом из них диагональ, как показано на рисунке. Получился ещё один, внутренний квадрат, площадь которого равна половине площади большого квадрата, то есть 2 (рис. 1). Эти элементарные рассуждения подвели нас к очень важному факту — существованию квадра та площадью 2. А теперь ответьте: чему равна длина стороны этого квадрата? Если взглянуть на древнюю вавилонскую табличку (рис. 2), которая датируется 1800–1600 годами до н. э., можно увидеть сходство с нашим рисунком! Кроме того, людям, знакомым с вавилонской арифметикой, сразу станет понятно, что зазубрины на этой табличке есть не что иное, как числа, записанные в вавилонской шестидесятеричной системе счисления.

Присмотримся к горизонтальной диагонали таблички. Там расставлены цифры: 1, 24, 51, 10. Учёные разгадали загадку: это очень точное приближение числа √2, записанное в шестидесятеричной системе счисления:

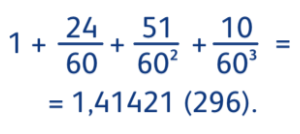
Почему √2 иррациональное число?

Несмотря на открытие числа √2, мысль, что оно отличается от других типов чисел, пришла лишь спустя 12 веков — пифагорейцам. Древнегреческий математик Пифагор, живший в VI веке до н. э., создал религиозно-философскую школу и учение, основывающееся в том числе на научном подходе к познанию мира. Уверенность пифагорейцев в божественной сущности чисел превратила арифметику в своего рода численную теологию, а математику сделала средством для изучения «божественного порядка». Пифагорейцы исследовали различные типы чисел, их взаимосвязи, искали числовые закономерности. Неудивительно, что они зало- жили основы современной теории чисел и символической алгебры.

Пифагор считал, что существует об- щая единица длины, достаточно малая и неделимая, — так сказать, квант числа. При этом одной из насущных проблем математики тех времён была необходимость сравнивать отрезки. Из предположения Пифагора вытекало, что любые отрезки можно сравнить и это отношение можно представить в виде несократимой дроби. Например, пусть есть два отрезка: AB и CD, а p — тот самый «квант числа».

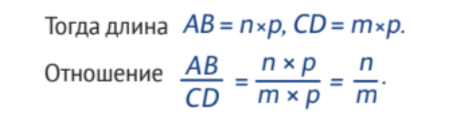
Но, как бывает в науке, в процессе поиска универсальной закономерности иногда обнаруживается явление, не поддающееся описанию и противоречащее сложившимся воззрениям. Как правило, такие случаи заставляют пересмотреть некоторые теории, что существенно расширяет границы области изучения. Так произошло и с пифагорейским представлением о числе.

Ученик Пифагора, Гиппас из Метапонта, решил применить теорему своего учителя, чтобы вычислить диагональ единичного квадрата. Результат был поразительным: длина диагонали оказалась таким числом, которое невозможно пред- ставить в виде отношения натуральных чисел. Оно было несоизмеримо со стороной квадрата, а также с любыми другими числами. Таким образом Гиппас доказал, что число, которое при возведении в квадрат даёт 2 (12 + 12 = 2), не является рациональным (лат. ratio — отношение, деление, дробь), и назвал его иррациональным. Доказательств иррациональности числа √2 великое множество. Алгебраические доказательства опирались на свойства чётных чисел и разложение на простые множители. Геометрические более разнообразны: тут и построения в прямоугольных треугольниках, и метод площадей.

Геометрическое доказательство

Пусть m √2 = n , где m:n — наименьшие возможные числа, не имеющие общих делителей. Тогда 2n²= m², то есть площадь квадрата со стороной m равна сумме площадей двух квадратов со сторонами n. Если меньшие квадраты поместить в противоположные углы большого квадрата, их пересечение даст нам новый квадрат со стороной m − 2(m − n) = 2n − m. Незакрытые участки квадрата также являются квадратами со стороной m − n. Из равенства площади квадрата со стороной m и суммы квадратов со стороной n мы получаем, что площадь участка плоскости, где квадраты накладываются друг на друга, равна площади незакрытых участков внутри квадрата, то есть (2n − m)²= 2(m − n)². Отсюда следует, что √2 = 2n − m : m − n . То есть число √2 может быть представлено в виде отношения целых чисел, меньших чем m и n, которые и так являлись наименьшими! Получили противоречие.

Алгебраическое доказательство

Если число √2 может быть выражено в виде дроби, то мы можем записать его в виде отношения натуральных чисел a и b, а именно √2 = a:b , причём a и b не имеют общих множителей (то есть дробь несократима). Домножим равенство на b и возведём обе его части в квадрат. Получим 2b²= a². Так как левая часть равенства чётная, то и a2 должно делиться на 2, а это возможно только при чётном a. Если a чётное, мы можем представить его как a = 2с. Но тогда 2b²= 4с², из чего следует, что b²= 2с², а это влечёт за собой чётность числа b. Итак, мы получили, что a и b — чётные числа, но это противоречит утверждению о том, что дробь a:b несократима. Это проти- воречие доказывает невозможность представить √2 в виде дроби.

Зри в корень из двух!

Несложно заметить: число √2 встречается там, где речь идёт о квадратах или удвоении площади. И где же это происходит? Начнём, пожалуй, с вещей, которые ежедневно попадают нам в руки. Таких, как бумага в принтере. Формат бумаги — стандартизованный размер бумажного листа. Все страны мира, кроме Канады и США, пользуются международным стандартом ISO 216. Все форматы бумаги ISO имеют одно и то же соотношение сторон, равное 1 ÷ √2, так называемому отношению Лихтенберга (немецкий учёный Георг Лихтенберг в 1768 году первый заметил преимущества использования бумажного листа с таким отношением сторон). Этот формат был создан в 1975 году на основе немецкого стандарта DIN 476 и отличается от него только бо́льшими допустимыми погрешностями. Базовый лист бумаги (А0) имеет площадь в 1 м2 и соотношение сторон 1 ÷ √2. Все остальные размеры получаются разрезанием длинной стороны на две равные части, то есть площадь следующего листа равна половине площади предыдущего. Такое соотношение сторон сохраняется для всех последующих меньших форматов.

Арифметически это связано с равенством √2:2= 1:√2. А именно: пусть стороны листа были x и √2x. Уменьшая вторую сторону в два раза и оставляя первую неизменной, мы уменьшаем площадь прямоугольника в два раза. Стороны стали x и √2х: 2 . Найдём теперь отношение меньшей стороны к большей:

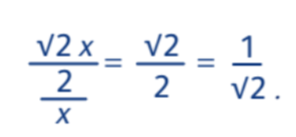
У фотографов тоже есть причина использовать число √2. Рассмотрим круг радиусом R. Его площадь равна πR2. Если мы хотим построить круг вдвое большей площади, как вы думаете, на какое число необходимо умножить радиус? А если вдвое меньшей — на какое разделить? Опять нас ждёт встреча с числом √2. Как это связано с фотографией? Когда мы снимаем в ручном режиме, то настраиваем фокус и экспозицию. Последняя определяется выдержкой и диафрагмой объектива — отверстием переменного радиуса, которое позволяет регулировать поток света, попадающего через объектив на плёнку или матрицу фотоаппарата.

Если свет яркий, отверстие диафрагмы уменьшают, чтобы не засветить кадр. Если же света мало — пасмурный день или вообще ночное время, — отверстие диафрагмы увеличивают, иначе кадр получится слишком тёмным. Разме- ры диафрагмы имеют фиксированное значение: при закрытии на одно деление площадь отверстия уменьшается вдвое, ну а радиус, соответственно, в √2 раз. Деле- ниям на шкале диафрагмы соответствуют так называемые диафрагменные числа: 2; 2,8; 4; 5,6; 8; 11; 16; 22 и так далее. За- кономерность неочевидна, но на самом деле это не что иное, как приближённые значения степеней числа √2 (округлённые почему-то не по математическим зако- нам):

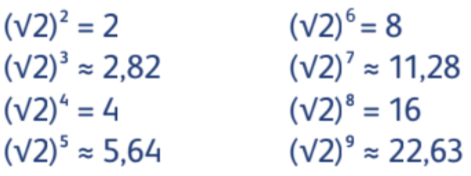
Это связано с тем, что если мы хотим получить ряд кругов площадью каждый вдвое меньше предыдущего, то радиус исходного круга мы должны будем последовательно делить на √2. Таким образом, отношение радиусов двух произвольных кругов из этого ряда всегда будет равно степени числа √2. Число √2 как пропорциональное от- ношение часто встречается в архитектуре: оно есть во всех квадратах, которые только можно начертить. Поэтому корень из двух занимает почётное место в искусстве, прежде всего в архитектуре и дизайне. В барселонском парке Гуэль, спроектированном великим Антонио Гауди, вместо чётких прямых линий мы наблюдаем очертания различной кривизны; центральным элементом паркового ансамбля является терраса, поддерживаемая греческими колоннами.

Изогнутый потолок, причудливые формы постройки могут вызвать ложное ощущение, что архитектор не придерживался какой-либо рациональной системы. Однако если посмотреть план сооружения, сразу видно, что его стабильность обеспечена геометрией квадратов, в вершины которых Гауди поместил вершины колонн. Ещё на чертеже можно заметить правильные восьмиугольники (октагоны), в которых тоже скрыто наше любимое число √2, ведь в каждом октагоне есть как минимум три квадрата. Слабость к правильному восьмиугольнику питали архитекторы разных эпох. Купол кафедрального флорентийского собора Санта-Мария-дель- Фьоре, Башня Ветров в Афинах, замок Кастель-дель-Монте на юге Италии, Капелла Карла Великого в немецком Ахене и многие другие постройки, всех не перечислить, имеют форму октагона.

Возможно, корень из двух не самое примечательное иррациональное число. Есть множество иррациональных чисел (π, экспонента е) и соотношений (напри- мер, золотое сечение), о которых можно рассказать больше интересного. Но важно понимать, что изучение таких чисел началось именно с √2. Его открытие перевернуло представления человечества о числе, положило начало изучению чисел как непрерывного множества и расширило возможности познания мира. В результате идея, что числа лежат в основе всех проявлений науки и техники, сегодня уже не вызывает сомнений.