Что может быть проще первого закона Ньютона? У него даже формулы нет! И нередко у школьника, начинающего изучение классической механики, складывается легковесное отношение к этому закону: мол, ничего серьёзного, надо просто выучить определение и «пятёрка» за урок обеспечена. На самом деле его важность для понимания механики трудно переоценить.
ИДЕЯ НЬЮТОНА И КУБИК ФЕЙНМАНА
Строго говоря, первый закон Ньютона (или закон инерции) законом не является. Это постулат, «исходное положение, допущение, принимаемое без доказательств, аксиома». Конечно, он появился не на пустом месте, а благодаря гениальным озарениям Г и Н и пересмотру прежних взглядов, господствовавших в естествознании многие столетия. Школьное определение: «Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно».
Такая формулировка, на первый взгляд, слишком сложна. Особенно в сравнении с собственными определениями Галилея и Ньютона: «Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Причины для такого усложнения есть. Для своего времени утверждение Галилея стало поистине революционным. В быту мы до сих пор повторяем точку зрения А: если предмет не трогать, то он и не будет двигаться.
Как объяснял один из выдающихся учёных нашего времени Р Ф, «попробуйте толкнуть кубик, стоящий на столе. Он остановится. Причина в том, что кубик трётся о стол, он не предоставлен самому себе. Нужно иметь очень богатое воображение, чтобы увидеть за этим принцип инерции».
На парашютиста действуют сила тяжести и сила сопротивления воздуха. Они равны по величине и противоположны по направлению, поэтому они компенсируют друг друга. В результате парашютист опускается вниз с постоянной скоростью примерно 5 м/с.
МАССА
Галилей, вне всякого сомнения, таким воображением обладал. Он «очистил» движение тела от любых воздействий на него (такие тела называются свободными) и установил важнейший факт: все без исключения материальные тела инертны, то есть способны сохранять скорость. Мера инертности, то есть способности сохранять свою скорость, — масса. Она скалярна (не имеет направления), всегда положительна и не является синонимом веса. Поэтому утверждения типа «мой вес не больше пятидесяти килограм мов» с точки зрения физики неверны. Вес — это сила, с которой тело действует на опору или подвес, при этом причина такого действия может быть разной.
ИСААК НЬЮТОН (1642–1727)
ГАЛИЛЕО ГАЛИЛЕЙ (1564–1642)
Подавляющее большинство окружающих нас тел «отягощено» неисчислимыми взаимодействиями, поэтому воззрения Аристотеля так долго не подвергались сомнению. Пожалуй, наиболее близки к объектам, движущимся по инерции, элементарные частицы в пучках ускорителей. Они практически не взаимодействуют друг с другом, летят в вакууме с большой скоростью, а масса их слишком мала.
Воздействия со стороны других тел могут компенсировать друг друга. В обычной жизни определяющим фактором, успешно «обманувшим» древнегреческих философов, является трение — сопротивление движению. Снизив его (замена трения скольжения трением качения, смазка, газовые или магнитные «подушки»), можно добиться «почти равномерного» движения, пренебрегая одними силами и компенсировав другие.
При всей своей математической «несолидности» первый закон Ньютона может дать много пищи для размышлений. В современной формулировке он начинается с упоминания об инерциальных системах отсчёта. Непонятно, почему сам Ньютон ни словом не обмолвился об этом, ведь основной задачей было как раз количественное описание движения, невозможное без полноценной системы отсчёта (тела отсчёта, связанной с ним системы координат и часов). Поэтому нынешняя формулировка полнее, чем ньютоновская. Она говорит о существовании особых систем отсчёта (СО), привязанных к свободным телам, движущимся с постоянной скоростью.
Аэрохоккей — игра, в которой трение скольжения практически сведено к нулю за счет применения пневматический «подушки»
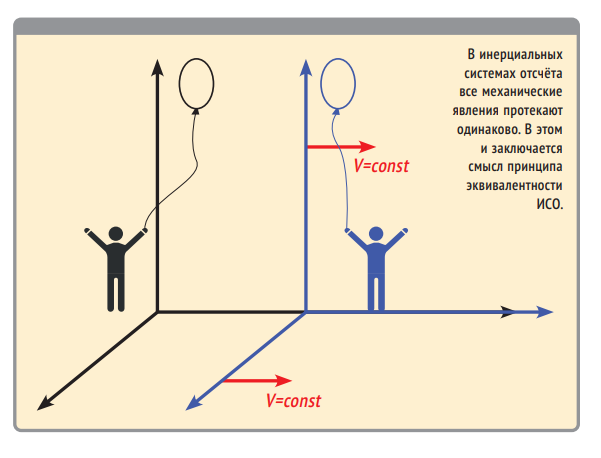
Но ведь таких тел может быть очень много! Совершенно верно. Следовательно, и возможных систем отсчёта — тоже. Мы можем выбирать наиболее подходящую СО в условиях конкретной задачи. А поможет нам в этом эквивалентность инерциальных систем отсчёта (ИСО): в любой из них законы механики выражаются одинаково.
РЕВОЛЮЦИЯ В ФИЗИКЕ
Позже попытка расширить принцип эквивалентности на электродинамику привела к «крушению» классической физики и созданию специальной теории относительности. Революция в физике началась с невинного вопроса: что же такое свет — частицы или волны? В некотором роде, корпускулярная теория в конце XIX века фактически оставалась не у дел. Система воззрений на свет как на волну прекрасно объясняла подавляющее большинство оптических явлений и отлично «работала» на практике. Оставалось ответить на «детский» вопрос: а в чём распространяются световые волны? Такой гипотетической средой стал эфир, равномерно заполняющий всё пространство и слабо проявляющий себя в иных взаимодействиях. Взяв за основу мировой эфир, мы получим преимущественную СО. В некотором смысле она перекликается с абсолютным пространством Ньютона, которое он считал естественным фундаментом мироздания. Но дальнейшие эксперименты доказали, что никакого эфира не существует, то есть абсолютную СО привязать не к чему.
Крах теории эфира ещё раз подтвердил верность принципа эквивалентности ИСО. В практических задачах часто в качестве ИСО берутся системы отсчёта, связанные с телами, движущимися с ускорением. Типичным примером такой СО является геоцентрическая (или лабораторная) система отсчёта, жёстко связанная с Землёй. Строго говоря, она таковой не является, но если учесть, что максимальное центростремительное ускорение, обусловленное вращением Земли, не превышает 0,5 % от ускорения свободного падения, то с достаточной степенью точности лабораторную СО можно считать инерциальной.
ИНТЕРЕСНЫЕ ВЫВОДЫ
Есть ещё несколько не столь очевидных, но весьма интересных выводов из первого закона. Так, изменение характера движения тела может служить своеобразным индикатором присутствия внешних сил, воздействующих на него. Попробуем воспроизвести цепочку рассуждений. Всем знакома праща — метательное оружие, применяемое с незапамятных времён. Это ремённая или верёвочная петля, в которую вложен камень, ядро или металлическая пуля массой до 400 г. Раскручивая пращу, метатель добивается всё большей и большей скорости ядра. В нужный момент, отпустив один из концов петли, человек посылает ядро по прямой с большой скоростью на расстояние до двухсот и более метров (просто бросить камень с такой силой невозможно). Перестав удерживать ядро пращей, мы превращаем его в свободное тело в системе «праща—ядро», и оно, в соответствии с первым законом, отправляется в полёт по инерции, стремясь сохранить свою скорость. Стало быть, движение по окружности свободным не является: скорость тела всё время меняет своё направление (то есть испытывает, говоря словами Ньютона, «изменение движения» — ускорение), и вынуждает его это делать натяжение верёвки, то есть центростремительная сила. То же самое происходит и с планетами, обращающимися вокруг Солнца. Только удерживаться на своих орбитах их заставляет не верёвка, а притяжение центральной звезды. В этом кроется коренное отличие от воззрений древнегреческих философов, считавших круг совершенной фигурой, а движение по окружности — естественным и не нуждающимся в каком-то воздействии.
Евклидово пространство является плоским в том смысле, что в нём справедлива евклидова геометрия
Первый закон Ньютона указывает — правда, неявно — на «плоскую» геометрию нашего пространства. Тело, движущееся по инерции, летит по прямой. Два таких невзаимодействующих тела с коллинеарными (то есть лежащими на параллельных прямых) скоростями никогда не столкнутся друг с другом, как и параллельные прямые никогда не пересекутся. Такие «плоские» трёхмерные пространства называются евклидовыми и описываются аксиомами «школьной» геометрии.